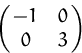Ähnliche Matrizen ![]() und
und
![]() haben die gleichen
Eigenwerte und besitzen (unter Berücksichtigung des Basiswechsels) die
gleichen Eigenvektoren:
haben die gleichen
Eigenwerte und besitzen (unter Berücksichtigung des Basiswechsels) die
gleichen Eigenvektoren:
Ist ![]() ein Eigenvektor von
ein Eigenvektor von ![]() zum Eigenwert
zum Eigenwert
![]() , dann ist
, dann ist ![]() Eigenvektor von
Eigenvektor von
![]() zum gleichen Eigenwert:
zum gleichen Eigenwert:
Für die Eigenvektoren gilt:
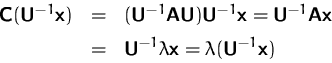
(Matrizen mit gleichen Eigenwerten müssen aber nicht notwendigerweise ähnlich sein.)
Wir wählen für unsere Abbildung eine Basis, sodaß die entsprechende Matrix
![]() möglichst einfach wird. Die einfachsten Matrizen sind
Diagonalmatrizen.
möglichst einfach wird. Die einfachsten Matrizen sind
Diagonalmatrizen.
Können wir immer eine Darstellung durch eine Diagonalmatrix finden?
M.a.W.: Ist ![]() ähnlich einer Diagonalmatrix?
ähnlich einer Diagonalmatrix?
Wir beschränken uns hier auf symmetrische Matrizen.
DEFINITION (SYMMETRISCHE MATRIX)
Eine ![]() -Matrix
-Matrix ![]() heißt
symmetrisch, falls
heißt
symmetrisch, falls
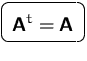
Die Eigenwerte und Eigenvektoren einer symmetrischen Matrix
![]() haben folgende wichtige Eigenschaften:
haben folgende wichtige Eigenschaften:
Betrachten wir die Transformationsmatrix
![]() .Wegen der Orthonormiertheit gilt
.Wegen der Orthonormiertheit gilt
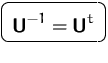
Für jeden Einheitsvektor ![]() gilt daher
gilt daher
![]()
Also
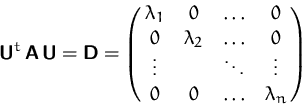
Jede symmetrische Matrix ist somit ähnlich zu einer Diagonalmatrix.
Jede symmetrische Matrix wird bezüglich einer Orthonormalbasis aus
Eigenvektoren zu einer Diagonalmatrix, deren Diagonalelemente die
Eigenwerte von ![]() sind.
Man nennt diesen Vorgang
Diagonalisieren.
sind.
Man nennt diesen Vorgang
Diagonalisieren.
Viele -- aber nicht alle -- nichtsymmetrischen Matrizen lassen
sich ebenfalls Diagonalisieren.
BEISPIEL
Wir wollen 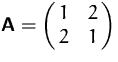 diagonalisieren.
diagonalisieren.
Das charakteristische Polynom ist
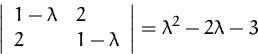
Die Eigenwerte sind daher
![]()
Die normierten Eigenvektoren sind
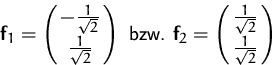
Bezüglich dieser Basis wird ![]() zur Diagonalmatrix
zur Diagonalmatrix