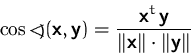Das innere Produkt (oder Skalarprodukt) zweier Vektoren
DEFINITION (INNERES PRODUKT, SKALARPRODUKT)
Das innere Produkt
(oder Skalarprodukt)
zweier Vektoren ![]() und
und ![]() ist
ist
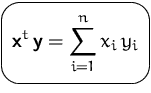
Zwei Vektoren heißen orthogonal, wenn
![]() .
.
(D.h. die beiden Vektoren stehen normal (senkrecht, im rechten Winkel) aufeinander).
BEISPIEL
Das innere Produkt von
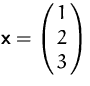 und
und
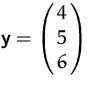 ist
ist
![]()
DEFINITION (NORM)
Die Norm (oder Länge) ![]() eines Vektors
eines Vektors ![]() ist
ist
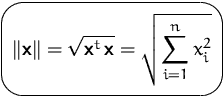
Ein Vektor ![]() heißt normiert, falls
heißt normiert, falls
![]() .
.
(D.h. der Vektor hat Länge 1).
BEISPIEL
Die Norm von 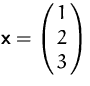 ist
ist
![]()
Die Norm mißt die Länge eines Vektors, das innere Produkt den Winkel zwischen zwei Vektoren.