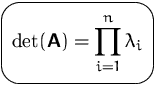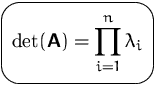previous: Diagonalisieren
up: Eigenwerte und Eigenvektoren
next: Eine geometrische Interpretation
- (1)
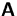 und
und 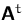 besitzen dieselben Eigenwerte.
besitzen dieselben Eigenwerte.
- (2)
- Seien
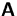 und
und 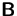
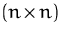 -Matrizen.
Dann besitzen die Matrizen
-Matrizen.
Dann besitzen die Matrizen 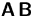 und
und 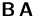 dieselben Eigenwerte.
dieselben Eigenwerte.
- (3)
- Ist
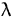 ein Eigenwert der regulären
Matrix
ein Eigenwert der regulären
Matrix 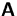 , dann ist
, dann ist 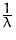 ein Eigenwert von
ein Eigenwert von 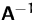 .
.
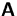 und
und 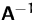 haben dieselben Eigenvektoren.
haben dieselben Eigenvektoren.
- (4)
- Ist
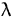 ein Eigenwert von
ein Eigenwert von 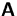 , dann ist
, dann ist
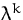 ein Eigenwert von
ein Eigenwert von 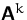 .
. - (5)
- Die Determinante einer
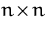 -Matrix
-Matrix 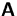 ist gleich
dem Produkt der Eigenwerte
ist gleich
dem Produkt der Eigenwerte 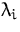 von
von 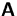 :
:
- (6)
- Die Summe der Eigenwerte
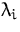 einer Matrix
einer Matrix 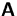 ist gleich der Summe der Diagonalelemente (der Spur
ist gleich der Summe der Diagonalelemente (der Spur
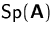 ) von
) von 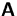 .
.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung