previous: Wie berechnet man Eigenwerte? up: Eigenwerte und Eigenvektoren next: Diagonalisieren

Wie berechnet man Eigenvektoren?

Wir können die Eigenvektoren $\mathsfbf{x}$ zum bekannten Eigenwert $\lambda$ durch Einsetzen in $(\mathsfbf{A}-\lambda\mathsfbf{I})\mathsfbf{x}= \mathsfbf{o}$ berechnen.

BEISPIEL
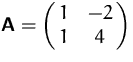Wir suchen die Eigenvektoren von $\mathsfbf{A}=\pmatrix{ 1 & -2\cr 1 & 4 }$ .

Die Eigenvektoren zum Eigenwert $\lambda_1=2$ erhalten wir aus

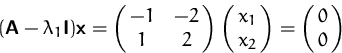
$\begin{displaymath} (\mathsfbf{A}-\lambda_1\mathsfbf{I})\mathsfbf{x}= \pmatrix{ -1 & -2\cr 1 & 2 }\pmatrix{ x_1 \cr x_2} = \pmatrix{ 0\cr 0} \end{displaymath}$

Als Lösung erhalten wir mittels Gauß-Elimination $x_2=\alpha$ und $x_1=-2\alpha$ , für ein $\alpha\in{\mathbb R}\setminus\{0\}$ , bzw. als Vektor
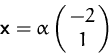
$\begin{displaymath} \mathsfbf{x} = \alpha\pmatrix{ -2\cr 1} \end{displaymath}$

Die Eigenvektoren sind daher 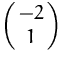$\pmatrix{ -2\cr 1}$ und jedes nichtverschwindende Vielfache davon.
Analog erhalten wir für die Eigenvektoren des zweiten Eigenwertes 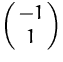$\lambda_2=3$ , $\pmatrix{ -1\cr 1}$ und jedes nichtverschwindende Vielfache davon.

Falls $\mathsfbf{x}$ ein Eigenvektor zum Eigenwert $\lambda$ ist, dann ist auch jedes Vielfache $\alpha\vec x$ ein Eigenvektor:

$\begin{displaymath} \mathsfbf{A}(\alpha\mathsfbf{x}) = \alpha(\mathsfbf{A}\mathsfbf{x}) = \alpha\lambda\mathsfbf{x} = \lambda(\alpha\mathsfbf{x})\end{displaymath}$

Falls $\mathsfbf{x}$ und $\mathsfbf{y}$ Eigenvektoren zum gleichen Eigenwert $\lambda$ sind, dann ist auch $\mathsfbf{x}+\mathsfbf{y}$ ein Eigenvektor

$\begin{displaymath} \mathsfbf{A}(\mathsfbf{x}+\mathsfbf{y}) = \mathsfbf{A}\math... ...bf{x} +\lambda\mathsfbf{y} = \lambda(\mathsfbf{x}+\mathsfbf{y})\end{displaymath}$

Die Menge aller Eigenvektoren zum Eigenwert $\lambda$ vereinigt mit dem Nullvektor ist daher ein Unterraum des ${\mathbb R}^n$ und wird als Eigenraum bezeichnet.

BEISPIEL
Gesucht sind die Eigenwerte und Eigenvektoren von

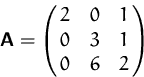
$\begin{displaymath} \mathsfbf{A}=\pmatrix{2 & 0 & 1\cr 0 & 3 & 1\cr 0 & 6 & 2} \end{displaymath}$

Wir bilden das charakteristische Polynom und berechnen dessen Nullstellen.
$\begin{displaymath} \begin{array} {rcl} \det(\mathsfbf{A}-\lambda\mathsfbf{I}) ... ...6)\\ [2ex] & = & (\lambda-2)\lambda(\lambda-5)=0 \end{array}\end{displaymath}$

Wir erhalten die Eigenwerte
$\begin{displaymath} \lambda_1=2\mbox{, }\lambda_2=0\mbox{ und } \lambda_3=5 \end{displaymath}$

Die Eigenvektoren zum Eigenwert $\lambda_3=5$ erhalten wir durch Lösen der Gleichung
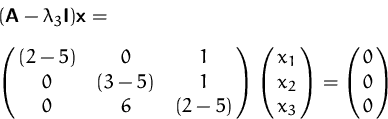
$\begin{displaymath} \begin{array} {l} (\mathsfbf{A}-\lambda_3\mathsfbf{I})\math... ...trix{ x_1\cr x_2\cr x_3}= \pmatrix{ 0\cr 0\cr 0} \end{array} \end{displaymath}$

Durch Gauß-Elimination erhalten wir
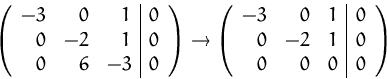
$\begin{displaymath} \left( \begin{array} {rrr\vert r} -3 & 0 & 1 & 0\\ 0 & -2 ... ...1 & 0\\ 0 & -2 & 1 & 0\\ 0 & 0 & 0 & 0 \end{array} \right) \end{displaymath}$
und somit $x_3=\alpha_3$ , $x_2=\frac{1}{2}\alpha_3$ und $x_1=\frac{1}{3}\alpha_3$ für ein beliebiges $\alpha_3\in{\mathbb R}\setminus\{0\}$ .
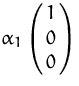Analog für $\lambda_1=2$ : $\alpha_1\pmatrix{1 \cr 0 \cr 0}$ .

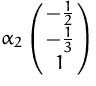und für $\lambda_2=0$ : $\alpha_2\pmatrix{-\frac{1}{2}\cr -\frac{1}{3}\cr 1}$ .