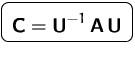Die Basis eines Vektorraumes und damit die Koordinatendarstellung eines Vektors ist nicht eindeutig.
Die Matrix ![]() einer linearen Abbildung
einer linearen Abbildung ![]() hängt ebenfalls von der verwendeten Basis ab.
hängt ebenfalls von der verwendeten Basis ab.
Sei nun ![]() die Matrix bezüglich der Basis
die Matrix bezüglich der Basis
![]() .Wie sieht nun die entsprechende Matrix
.Wie sieht nun die entsprechende Matrix ![]() bezüglich der
Basis
bezüglich der
Basis ![]() aus?
aus?
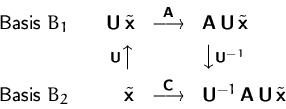
![]()
DEFINITION (ÄHNLICHE MATRIZEN)
Zwei ![]() -Matrizen
-Matrizen ![]() und
und ![]() heißen
ähnlich, falls es eine
invertierbare Matrix
heißen
ähnlich, falls es eine
invertierbare Matrix ![]() gibt, mit
gibt, mit