Seien ![]() Elemente
eines Vektorraumes
Elemente
eines Vektorraumes ![]() .
.
Wir betrachten die Menge aller Linearkombinationen
![]() dieser Elemente. Diese Menge wird mit
dieser Elemente. Diese Menge wird mit
![]()
bezeichnet und heißt der von ![]() aufgespannte Unterraum von
aufgespannte Unterraum von ![]() .
.
DEFINITION (UNTERRAUM)
Ein Unterraum (oder Teilraum) ist eine
Teilmenge eines Vektorraumes, die selbst wieder einen Vektorraum
bildet.
BEISPIEL
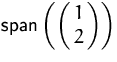 ist eine Gerade durch
Ursprung im
ist eine Gerade durch
Ursprung im ![]() .
.
BEISPIEL
Seien 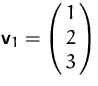 ,
, 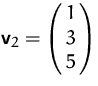 ,
, 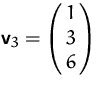 .
.
Dann ist
![]() .
.
Eine Menge von Vektoren
![]() erzeugt einen Vektorraum
erzeugt einen Vektorraum ![]() ,falls
,falls
![]()
Sind diese Vektoren linear unabhängig, so heißt diese Menge eine Basis des Vektorraumes.
Die Anzahl dieser Vektoren ist die Dimension
des Vektorraumes:
![]()
BEISPIEL
Die drei Vektoren ![]() ,
, ![]() ,
, ![]() im
obigen Beispiel bilden eine Basis des
im
obigen Beispiel bilden eine Basis des ![]() und
und ![]() .
.
Die Basis eines Vektorraumes ist nicht eindeutig bestimmt.
BEISPIEL
Die Einheitsvektoren mit drei
Komponenten ![]() bilden eine Basis des
bilden eine Basis des ![]() .
. ![]() .
.
Diese Basis heißt die kanonische Basis des ![]() .
.
Die Koordinaten ![]() eines Vektors
eines Vektors ![]() bezüglich einer Basis
bezüglich einer Basis
![]() erhalten wir durch Lösen des Gleichungssystems
erhalten wir durch Lösen des Gleichungssystems
![]()
In Matrixschreibweise:
![]()
wobei
![]() die Basisvektoren als Spaltenvektoren enthält.
die Basisvektoren als Spaltenvektoren enthält.
BEISPIEL
Wir suchen die Koordinaten von
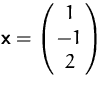 bezüglich
bezüglich
der Basis
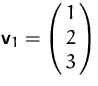 ,
, 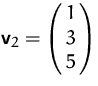 ,
, 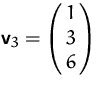 .
.
Wir lösen das Gleichungssystem
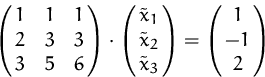
mittels Gaußschem Eliminationsverfahren.
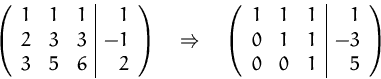
![]()
![]() ,
, ![]() und
und ![]() .
.
Die Koordinaten bezüglich dieser Basis sind
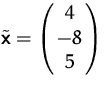 .
.