In unserem Leontief-Modell
haben wir jeder Produktion ![]() einen internen Verbrauch
einen internen Verbrauch
![]() durch
durch
![]()
Die Menge aller Vektoren ![]() mit
mit ![]() Komponenten bezeichnen
wir mit
Komponenten bezeichnen
wir mit
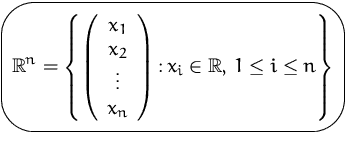
und wird als
![]() -dimensionaler (reeller)Vektorraum bezeichnet
-dimensionaler (reeller)Vektorraum bezeichnet
DEFINITION (VEKTORRAUM)
Ein Vektorraum ![]() ist eine Menge, deren Elemente
sich addieren und skalarmultiplizieren
lassen, wobei die Summe von Vektoren und das
Vielfache eines Vektors wieder Elemente der Menge sind.
Die Elemente so eines Vektorraumes sind (heißen) Vektoren.
ist eine Menge, deren Elemente
sich addieren und skalarmultiplizieren
lassen, wobei die Summe von Vektoren und das
Vielfache eines Vektors wieder Elemente der Menge sind.
Die Elemente so eines Vektorraumes sind (heißen) Vektoren.
BEISPIEL
Nach dieser Definition ist die Menge aller ![]() -Matrizen
-Matrizen
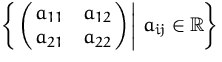 ein Vektorraum.
ein Vektorraum.
BEISPIEL
Die Menge aller Polynome vom Grad kleiner gleich 2,
![]()