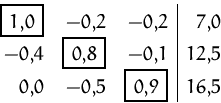
Mit Hilfe des Gaußschen Eliminationsverfahrens können die Lösungen eines Gleichungssystems gefunden werden bzw. kann festgestellt werden, ob das Gleichungssystem inkonsistent ist.
Zur besseren Übersicht können die Variablenbezeichnungen weggelassen
werden.
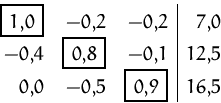
Durch Umformungen bringen wir das Schema in die
Staffelform.
Die Staffelform hat die Eigenschaft, daß die Anzahl der Elemente gleich 0, die ganz auf der linken Seite stehen, von Zeile zu Zeile um mindestens eins zunimmt.
Es sind (nur) die folgenden Operationen erlaubt:
| Multiplikation einer Zeile mit einer Konstanten
( |
|
| Addition des Vielfachen einer Zeile zu einer anderen Zeile. | |
| Vertauschen zweier Zeilen. |
Diese Operationen lassen die Lösung des Gleichungssystems unverändert.
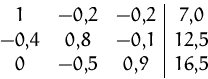
Wir addieren zunächst das ![]() -fache der ersten Zeile
zur zweiten Zeile. Wir schreiben dafür kurz:
-fache der ersten Zeile
zur zweiten Zeile. Wir schreiben dafür kurz:
![]()
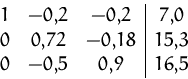
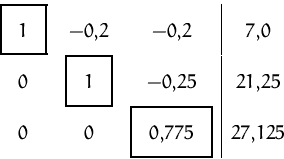
Aus der dritten Zeile erhalten wir direkt:
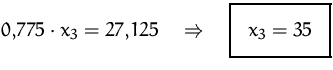
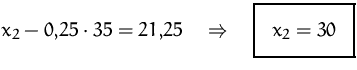
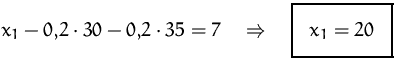
Die Lösungsmenge besteht daher aus einem einzigen Punkt:
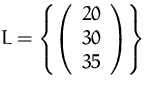
BEISPIEL
Suchen die Lösung des Gleichungssystems:
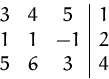
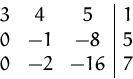
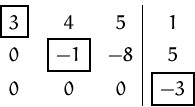
Aus der drittem Zeile erhalten wir
![]() , ein Widerspruch.
Das Gleichungssystem ist
inkonsistent:
, ein Widerspruch.
Das Gleichungssystem ist
inkonsistent:
![]()
BEISPIEL
Suchen die Lösung des Gleichungssystems:
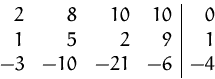
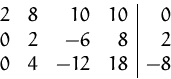
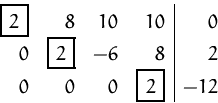
Dieses Gleichungssystem hat unendlich viele Lösungen. Das können wir daran erkennen, daß nach Erreichen der Staffelform mehr Variablen als Gleichungen übrigbleiben.
Die Lösung 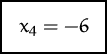 läßt sich unmittelbar aus der dritten Zeile
ablesen.
läßt sich unmittelbar aus der dritten Zeile
ablesen.
Durch Rücksubstitution erhalten wir
Wir setzen ![]() gleich einem ,,Parameter``
gleich einem ,,Parameter`` ![]() :
: 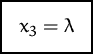 , und erhalten
, und erhalten
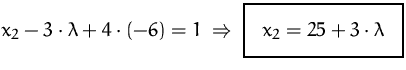
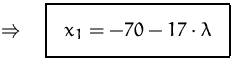
Jede Belegung des Parameters ![]() liefert eine gültige Lösung:
liefert eine gültige Lösung:
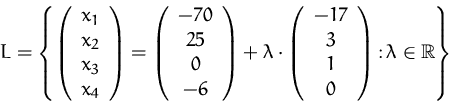
Wir hätten im obigen Beispiel genauso ![]() setzen können,
und daraus das
setzen können,
und daraus das ![]() ausgerechnet:
ausgerechnet:
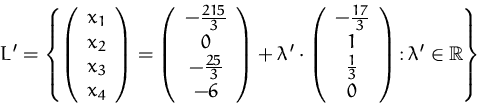
Die beiden Mengen sind aber gleich, ![]() . Es handelt sich dabei
nur zwei verschiedene -- aber äquivalente --
Parameterdarstellungen der selben Gerade.
. Es handelt sich dabei
nur zwei verschiedene -- aber äquivalente --
Parameterdarstellungen der selben Gerade.
Die Lösungsmenge ist immer eindeutig bestimmt, die Darstellung der
Lösung hingegen nicht.