previous: Vorteile up: Matrizen und Vektoren next: Rang einer Matrix

Lineare Unabhängigkeit

Wir können Vektoren $\mathsfbf{x}_1, \ldots, \mathsfbf{x}_n$ mit Zahlen $\alpha_1, \ldots, \alpha_n$ multiplizieren und die resultierenden Vektoren addieren. Auf diese Weise erhalten wir eine Linearkombination der Vektoren $\mathsfbf{x}_1, \ldots, \mathsfbf{x}_n$ :

$\begin{displaymath} \mathsfbf{x} = \alpha_1\,\mathsfbf{x}_1 + \cdots + \alpha_n\,\mathsfbf{x}_n\end{displaymath}$

BEISPIEL
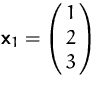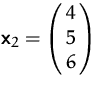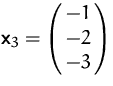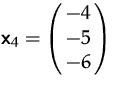$\mathsfbf{x}_1=\pmatrix{1\cr 2\cr 3}$ , $\mathsfbf{x}_2=\pmatrix{4\cr 5\cr 6}$ , $\mathsfbf{x}_3=\pmatrix{-1\cr -2\cr -3}$ , $\mathsfbf{x}_4=\pmatrix{-4\cr -5\cr -6}$ .

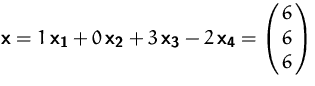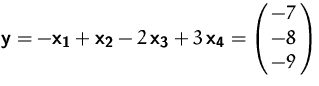
Dann sind $\mathsfbf{x} = 1\,\mathsfbf{x_1} + 0\,\mathsfbf{x_2} + 3\,\mathsfbf{x_3} - 2\,\mathsfbf{x_4} = \pmatrix{6\cr 6\cr 6}$ und $\mathsfbf{y} = -\mathsfbf{x_1} + \mathsfbf{x_2} - 2\,\mathsfbf{x_3} + 3\,\mathsfbf{x_4} = \pmatrix{-7\cr -8\cr -9}$

Linearkombinationen der Vektoren $\mathsfbf{x_1}$ , $\mathsfbf{x_2}$ , $\mathsfbf{x_3}$ und $\mathsfbf{x_4}$ .

Umgekehrt:

Die Vektoren $\mathsfbf{x}$ und $\mathsfbf{y}$ lassen sich als Linearkombinationen dieser Vektoren ausdrücken.

Diese Darstellung ist aber nicht immer eindeutig.

BEISPIEL FORTSETZUNG
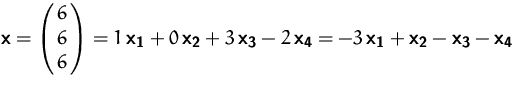
$\mathsfbf{x}=\pmatrix{6\cr 6\cr 6} = 1\,\mathsfbf{x_1} + 0\,\mathsfbf{x_2} + 3... ...f{x_4} = -3\,\mathsfbf{x_1} + \mathsfbf{x_2} - \mathsfbf{x_3} - \mathsfbf{x_4}$

Die Vektoren $\mathsfbf{x}_1,\ldots, \mathsfbf{x}_4$ in diesem Beispiel sind linear abhängig.

DEFINITION (LINEAR UNABHäNGIG)
Falls das Gleichungssystem

$\mbox{\ovalbox{$\displaystyle x_1\,\mathsfbf{v}_1 + x_2\,\mathsfbf{v}_2 +\cdots + x_n\,\mathsfbf{v}_n=\mathsfbf{0}$}}$

nur die Lösung $x_1=x_2=\cdots=x_n=0$ besitzt,
heißen die Vektoren $\mathsfbf{v}_1,\,\mathsfbf{v}_2,\,\ldots,\,\mathsfbf{v}_n$ linear unabhängig.
Sie heißen linear abhängig, wenn das Gleichungssystem andere Lösungen besitzt.

Sind Vektoren linear abhängig, dann läßt sich ein Vektor (aber nicht notwendigerweise jeder!) als Linearkombination der anderen Vektoren darstellen.

Zur Bestimmung der linearen Unabhängigkeit von Vektoren eignet sich folgendes Verfahren:

(1)	Wir fassen die Vektoren als Spaltenvektoren einer Matrix auf.
(2)	Wir bringen die Matrix mit den Umformungsschritten des Gaußschen Eliminationsverfahrens in die Staffelform.
(3)	Wir zählen die Zeilen, die ungleich dem Nullvektor sind (d.h. mindestens ein Koeffizient in der Zeile muß ungleich Null sein).
(4)	Ist diese Anzahl gleich der Anzahl der Vektoren, so sind diese Vektoren linear unabhängig. Ist sie kleiner, so sind die Vektoren linear abhängig.

BEISPIEL
Sind die Vektoren

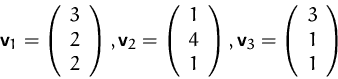
$\begin{displaymath} \mathsfbf{v}_1=\left(\begin{array} {c}3\\ 2\\ 2 \end{array}\... ...sfbf{v}_3=\left(\begin{array} {c}3\\ 1\\ 1 \end{array}\right) \end{displaymath}$

linear unabhängig?
(1) Wir bringen diese drei Vektoren in Matrixform:
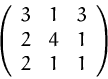
$\begin{displaymath} \left( \begin{array} {ccc} 3 & 1 & 3 \\ 2 & 4 & 1 \\ 2 & 1 & 1 \\ \end{array} \right) \end{displaymath}$

(2) Durch Umformung erhalten wir
$\begin{displaymath} Z2\leftarrow 3\times Z2- 2\times Z1, Z3\leftarrow 3\times Z3- 2\times Z1\end{displaymath}$

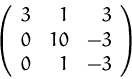
$\begin{displaymath} \left( \begin{array} {rrr} 3 & 1 & 3 \\ 0 & 10 & -3 \\ 0 & 1 & -3 \\ \end{array} \right) \end{displaymath}$

$\begin{displaymath} Z3\leftarrow 10\times Z3-Z2\end{displaymath}$

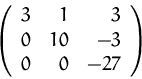
$\begin{displaymath} \left( \begin{array} {rrr} 3 & 1 & 3 \\ 0 & 10 & -3 \\ 0 & 0 & -27 \\ \end{array} \right) \end{displaymath}$

(3)(4) Die Anzahl der von Null verschiedenen Zeilen () stimmt mit der Anzahl der Vektoren () überein. Die drei Vektoren $\mathsfbf{v}_1$ , $\mathsfbf{v}_2$ und $\mathsfbf{v}_3$ sind daher linear unabhängig.

BEISPIEL
Sind die Vektoren

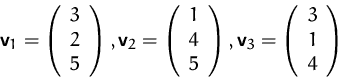
$\begin{displaymath} \mathsfbf{v}_1=\left(\begin{array} {c}3\\ 2\\ 5 \end{array}\... ...sfbf{v}_3=\left(\begin{array} {c}3\\ 1\\ 4 \end{array}\right) \end{displaymath}$

linear unabhängig?
(1) Wir bringen diese drei Vektoren in Matrixform:
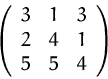
$\begin{displaymath} \left( \begin{array} {ccc} 3 & 1 & 3 \\ 2 & 4 & 1 \\ 5 & 5 & 4 \\ \end{array} \right) \end{displaymath}$
(2) Durch Umformung erhalten wir
$\begin{displaymath} Z2\leftarrow 3\times Z2- 2\times Z1, Z3\leftarrow 3\times Z3- 5\times Z1\end{displaymath}$

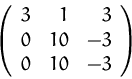
$\begin{displaymath} \left( \begin{array} {rrr} 3 & 1 & 3 \\ 0 & 10 & -3 \\ 0 & 10 & -3 \\ \end{array} \right) \end{displaymath}$

$\begin{displaymath} Z3\leftarrow Z3-Z2\end{displaymath}$

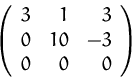
$\begin{displaymath} \left( \begin{array} {rrr} 3 & 1 & 3 \\ 0 & 10 & -3 \\ 0 & 0 & 0 \\ \end{array} \right) \end{displaymath}$

(3)(4) Die Anzahl der von Null verschiedenen Zeilen (2) ist kleiner als die Anzahl der Vektoren (3). Die drei Vektoren $\mathsfbf{v}_1$ , $\mathsfbf{v}_2$ und $\mathsfbf{v}_3$ sind daher linear abhängig.