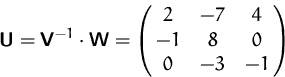Wie können wir eine Basis für den ![]() eine andere Basis
umformen?
eine andere Basis
umformen?
Seien ![]() und
und
![]() zwei Basen für den
zwei Basen für den ![]() .
.
Die Vektoren ![]() müssen sich als Linearkombination der
Basisvektoren
müssen sich als Linearkombination der
Basisvektoren ![]() darstellen lassen.
Etwa
darstellen lassen.
Etwa
![]()
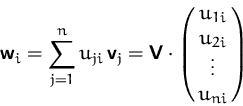
Setzen
![]() und
und
![]() :
:
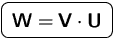
Die Matrix ![]() heißt Transformationsmatrix.
heißt Transformationsmatrix.
Sie ist nicht singulär.
Es gibt auch eine Basistransformation von ![]() nach
nach
![]() .
.
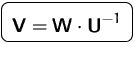
Wie änderen sich nun die Koordinaten ![]() eines Vektors
eines Vektors
![]() beim Basiswechsel?
beim Basiswechsel?
Sei ![]() die Kordinatendarstellung von
die Kordinatendarstellung von ![]() bezüglich der Basis
bezüglich der Basis ![]() ,
,![]() bez.
bez. ![]() .
.
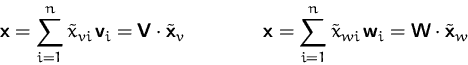
![]()
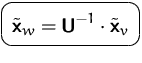
Die Transformationsmatrix ![]() können wir leicht aus
können wir leicht aus
![]() berechnen:
berechnen:
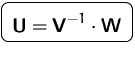
BEISPIEL
Transformationsmatrix für den Basiswechsel von
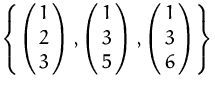 in
in
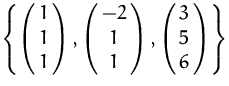 .
.
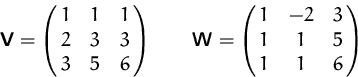
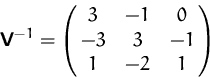
Lösung: