DEFINITION (LOKALES EXTREMUM)
![]() heißt
lokales Maximum (vgl.)
der Funktion
heißt
lokales Maximum (vgl.)
der Funktion ![]() , falls für alle
, falls für alle ![]() in
einer Umgebung von
in
einer Umgebung von ![]() ,
, ![]() , gilt:
, gilt: ![]() .
.
![]() heißt lokales Minimum,
falls
heißt lokales Minimum,
falls ![]() .
.
Alle lokalen Extrema einer differenzierbaren Funktion sind stationäre Punkte.
DEFINITION (STATIONäRER PUNKT)
Ein Punkt ![]() heißt
stationärer Punkt der Funktion
heißt
stationärer Punkt der Funktion
![]() falls
falls
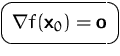
![]()
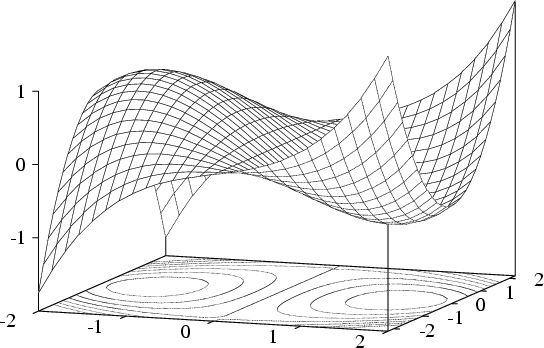
BEISPIEL
Suche alle stationären Punkte von
![]()
LöSUNG:
Bilde alle ersten partiellen Ableitungen, setze diese Null und löse das Gleichungssystem.
![\begin{displaymath}
\begin{array}
{llllll}
(I)& f_x &=& \frac{1}{2}\,x^2 - 1 + ...
... [1ex]
(II)& f_y &=& \frac{1}{2}\,x\,y & = & 0\\ \end{array} \end{displaymath}](img1318.gif)
Durch Eingesetzt in ![]() erhalten wir daraus
erhalten wir daraus
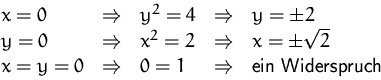
![]()
![]()
Mit Hilfe der Definitheit der Hesse-Matrix können wir bestimmen (vgl.), welche stationären Punkte Maxima , Minima oder Sattelpunkte sind (vgl.).
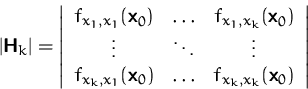
![]() ist ein
lokales Maximum von
ist ein
lokales Maximum von ![]() .
.
![]() ist ein
Sattelpunkt von
ist ein
Sattelpunkt von ![]() .
.
Wir haben in diesem Verfahren festgestellt, ob ![]() in einer Umgebung
des stationären Punktes
in einer Umgebung
des stationären Punktes ![]() streng konvex oder
streng konkav ist (vgl.).
streng konvex oder
streng konkav ist (vgl.).
Im Falle einer Funktion ![]() in zwei Variablen
vereinfacht sich (3) zu:
in zwei Variablen
vereinfacht sich (3) zu:
| Keine Aussage möglich |
Wir könnten die stationären Punkte von ![]() auch mit Hilfe der
Eigenwerte der Hesse-Matrix charakterisieren
(vgl.).
auch mit Hilfe der
Eigenwerte der Hesse-Matrix charakterisieren
(vgl.).
![\begin{figure}
\makebox[0pt][l]{\epsfxsize=12cm\epsfbox{figures/Extrema_Stationa...
...]{\epsfxsize=10cm\epsfbox{figures/Extrema_StationaerePunkte.1b.eps}}\end{figure}](img1339.gif)
![\begin{figure}
\makebox[0pt][l]{\epsfxsize=12cm\epsfbox{figures/Extrema_Stationa...
...]{\epsfxsize=10cm\epsfbox{figures/Extrema_StationaerePunkte.2b.eps}}\end{figure}](img1340.gif)
![\begin{figure}
\makebox[0pt][l]{\epsfxsize=12cm\epsfbox{figures/Extrema_Stationa...
...]{\epsfxsize=10cm\epsfbox{figures/Extrema_StationaerePunkte.3b.eps}}\end{figure}](img1341.gif)
![\begin{figure}
\makebox[0pt][l]{\epsfxsize=12cm\epsfbox{figures/Extrema_Stationa...
...]{\epsfxsize=10cm\epsfbox{figures/Extrema_StationaerePunkte.4b.eps}}\end{figure}](img1342.gif)
BEISPIEL (FORTSETZUNG)
(1) Hesse-Matrizen der Funktion
![]()
![$\mathsfbf{H}_f(\mathsfbf{x}) =
\pmatrix{ f_{xx}(\mathsfbf{x}) & f_{xy}(\mathsf...
...\frac{1}{2}\,y \\ [0.7ex]
\frac{1}{2}\,y & \frac{1}{2}\,x
\end{array} \right)$](img1344.gif)
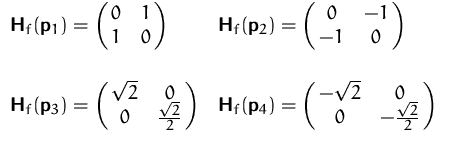
(2) + (3) Die Hauptminoren und deren Vorzeichen sind
![]() :
: ![]()
![]() Sattelpunkt
Sattelpunkt
![]() :
: ![]()
![]() Sattelpunkt
Sattelpunkt
![]() :
: ![]() ,
, ![]()
![]() lokales Minimum
lokales Minimum
![]() :
: ![]() ,
, ![]()
![]() lokales Maximum
lokales Maximum
BEISPIEL
Wir suchen die Extrema der Funktion
![]()
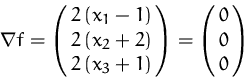
Der einzige stationäre Punkt ist ![]() .
.
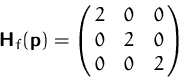
Alle Hauptminoren sind positiv:
![]() ,
, ![]() ,
, ![]()
![]()
![]() ist ein lokales Minimum.
ist ein lokales Minimum.