Sei
DEFINITION (QUADRATISCHE FORM)
Sei ![]() eine symmetrische Matrix.
Die Funktion
eine symmetrische Matrix.
Die Funktion
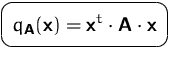
BEISPIEL
Sei 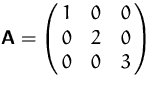 . Dann ist
. Dann ist
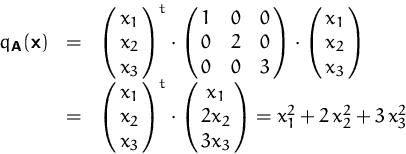
BEISPIEL
Sei 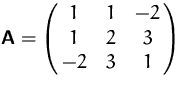 . Dann ist
. Dann ist
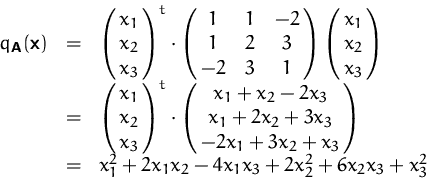
Allgemein gilt für eine ![]() -Matrix
-Matrix ![]() :
:
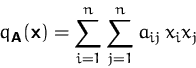
DEFINITION (DEFINITHEIT)
Eine quadratische Form ![]() heißt
heißt
Eine Matrix ![]() heißt positiv (negativ)
definit (semidefinit), wenn die entsprechende
quadratische Form positiv (negativ)
definit (semidefinit) ist.
heißt positiv (negativ)
definit (semidefinit), wenn die entsprechende
quadratische Form positiv (negativ)
definit (semidefinit) ist.
Jede symmetrische Matrix ist diagonalisierbar.
Sei ![]() eine Orthonormalbasis des
eine Orthonormalbasis des
![]() aus Eigenvektoren von
aus Eigenvektoren von ![]() . Dann gilt für jeden
Vektor
. Dann gilt für jeden
Vektor ![]() :
:
![]()
Für die quadratische Form erhalten wir dann
![\begin{displaymath}
\begin{array}
{rcl}
q_\mathsfbf{A}(\mathsfbf{x})
&=&
\mat...
...sfbf{v}_j\\ [1ex]
&=&
\sum_{i=1}^n a_i^2 \lambda_i\end{array}\end{displaymath}](img604.gif)
| Die quadratische Form |
| positiv definit, wenn alle |
| positiv semidefinit, wenn alle |
| negativ definit, wenn alle |
| negativ semidefinit, wenn alle |
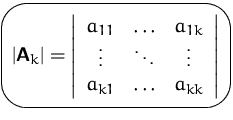
DEFINITION (HAUPTMINOR)
Sei ![]() eine symmetrische
eine symmetrische ![]() -Matrix. Dann
heißt die Determinanten der Untermatrix
-Matrix. Dann
heißt die Determinanten der Untermatrix
![]() -te Hauptminor von
-te Hauptminor von ![]() .
.
Mit Hilfe der Hauptminoren können wir ebenfalls die Definitheit einer quadratische Form feststellen.
| Eine quadratische Form |
| positiv definit, wenn alle |
| negativ definit, wenn für alle |
| Falls |
BEISPIEL
Gesucht ist die Definitheit der Matrix
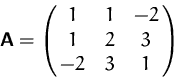
![]()
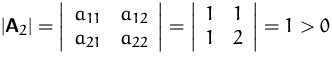
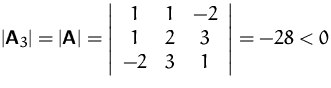
![]() und
und ![]() sind indefinit.
sind indefinit.
BEISPIEL
Gesucht ist die Definitheit der Matrix
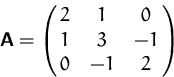
![]() ,
,
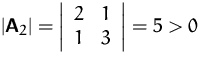 ,
,
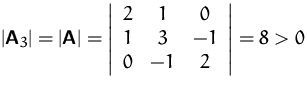 .
.
Alle Hauptminoren sind ![]() ,
, ![]()
![]() und
und ![]() sind positiv definit.
sind positiv definit.
Die Bedingung für Semidefinitheit ist nicht so einfach.
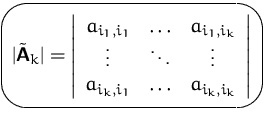
wobei ![]() .
.
| Eine quadratische Form |
| positiv semidefinit, wenn alle |
| negativ semidefinit, wenn alle |
| indefinit in allen anderen Fällen. |
BEISPIEL
Die allgemeinen Hauptminoren ![]() der Matrix
der Matrix
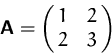
![]() und 3
und 3
sowie
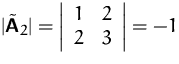 .
.
Die Matrix ist somit indefinit.
Jede positiv definite Matrix ist auch positiv semidefinit
(aber nicht umgekehrt).