previous: Lokale und globale Extremwerte up: Lokale und globale Extremwerte next: Berechnung der lokalen Extrema

Was sind Extremwerte?  

 

DEFINITION (LOKALES EXTREMUM)
$x_0\in D$ heißt  lokales Maximum der Funktion $f\colon D\to{\mathbb R}$, falls für alle $x$ in einem Intervall $(x_0-\varepsilon,x_0+\varepsilon)$ gilt: $f(x)\leq f(x_0)$.

$x_0$ heißt  lokales Minimum, falls $f(x)\geq f(x_0)$.

D.h. die Maximumseigenschaft gilt nur regional in der Nähe des lokalen Maximums.

 

DEFINITION (GLOBALES EXTREMUM)
$x_0\in D$ heißt  globales Maximum der Funktion $f\colon D\to{\mathbb R}$, falls für alle $x$ im Definitionsbereich gilt:

$$f(x)\leq f(x_0)$$

$x_0$ heißt  globales Minimum, falls $f(x)\geq f(x_0)$.

Jedes globale Maximum ist auch ein lokales Maximum. Umgekehrt kann ein lokales Maximum ein globales Maximum sein, muß aber nicht.

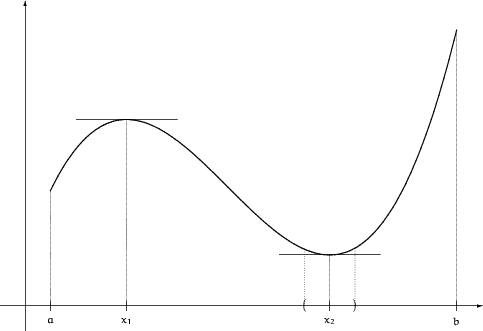
BEISPIEL
Extremwerte der Funktion

$f\colon[\,0{,}5;8{,}5\,]\to{\mathbb R},\, x\mapsto \frac{1}{12}\,x^3-x^2+3\,x+1$

Lokale Minima in $a$ und $x_2$, lokale Maxima in $x_1$ und $b$.

Globales Minimum in $x_2$, globales Maximum in $b$.