previous: Zinsen up: Folgen und Reihen next: Kredite

Renten (nachschüssig)  

Auf ein Bausparbuch wird am 31. Dezember jeden Jahres ein Betrag von $K$ Geldeinheiten eingezahlt. Die Verzinsung beträgt $p$ (%).
Wie groß ist das Guthaben nach 5 Jahren?

LöSUNG:

Die Guthaben aus den einzelnen Zahlungen (die aufgezinsten Einzahlungen) bilden eine geometrische Folge:

Guthaben aus der Einzahlung im $i-ten$ Jahr:

$$K_i = K\cdot q^{i-1}\qquad\mbox{mit }q=1+p$$

Das Gesamtguthaben $E_5$ ergibt sich aus der Summe dieser Folgeglieder:

$$\begin{array} {rcl} E_5 & = & K_1+K_2+K_3+K_4+K_5 = \\ & = &... ...t q^0+K\cdot q^1+K\cdot q^2+K\cdot q^3+K\cdot q^4\\ \end{array}$$

Eine Zahlung, die in gleicher Höhe in regelmäßigen Abständen erfolgt, heißt eine  Rente.
Wird die Rente jeweils zum Ende einer Periode bezahlt, so heißt sie  nachschüssig.

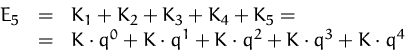
Der  Endwert einer Rente ist die Summe aller Zahlungen auf den Endzeitpunkt der Rente aufgezinst.

Sei $R$ die Rente, $p$ die Verzinsung und $n$ die Anzahl der Zahlungen so ist der Endwert nach der Summenformel für geometrische Reihen gleich

$\mbox{\ovalbox{$\displaystyle E_n=R\cdot\frac{q^n-1}{q-1}$}}$

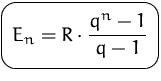
Der  Barwert ist die Summe aller Rentenzahlungen abgezinst auf den Beginn der Rente abgezinst. Er wird durch Abzinsung des Endwertes für $n$ Perioden berechnet.

$\mbox{\ovalbox{$\displaystyle B_n=\frac{E_n}{q^n} = R\cdot\frac{q^n-1}{q^n(q-1)}$}}$

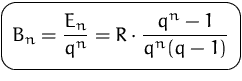
Unter der  ewigen Rente verstehen wir eine Rente, die unendlich oft gezahlt wird. Ihr Endwert ist immer unendlich. Ihr Barwert läßt sich durch den Grenzübergang der Anzahl der Zahlungen $n$ berechnen:

$\mbox{\ovalbox{$\displaystyle B_\infty=\lim_{n\to\infty} B_n = \frac{R}{q-1}$}}$

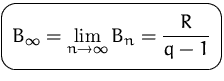
BEISPIEL
Gesucht ist der Bar- und Endwert einer jährlichen Rente von 5000 Geldeinheiten für 20 Jahre bei einer Verzinsung von 6%. Wie hoch wäre der Barwert für eine ewige Rente gleicher Höhe und Verzinsung?

$R=5000$, $n=20$, $p=0{,}06$, $q=1+p=1{,}06$.

$$E_{20}=5000\cdot\frac{1{,}06^{20}-1}{1{,}06-1}\approx 183\,927{,}96$$ Endwert: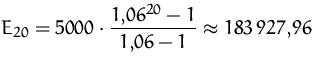

$$B_{20}=\frac{E_{20}}{1{,}06^{20}}\approx 57\,349{,}61$$ Barwert: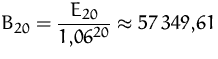

$$B_\infty=\frac{5000}{1{,}06-1}\approx 83\,333{,}33$$ ewige Rente: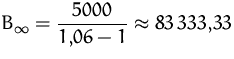