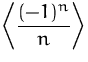 :
:
Betrachten wir die Folge
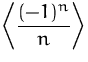 :
:

Die Folgeglieder ,,streben`` mit wachsendem ![]() gegen 0.
Wir sagen, die Folge
gegen 0.
Wir sagen, die Folge ![]() konvergiert gegen .
konvergiert gegen .
DEFINITION (LIMES)
Eine Zahl ![]() heißt
Grenzwert (oder Limes)
einer Folge
heißt
Grenzwert (oder Limes)
einer Folge ![]() , wenn es für jedes
noch so kleine Intervall
, wenn es für jedes
noch so kleine Intervall ![]() ein
ein ![]() gibt, sodaß
gibt, sodaß ![]() für alle
für alle
![]() (m.a.W.: alle Folgeglieder ab
(m.a.W.: alle Folgeglieder ab ![]() liegen im Intervall).
liegen im Intervall).
Eine Folge, die einen Grenzwert besitzt, heißt konvergent. Sie konvergiert gegen ihren Grenzwert.
Wir schreiben dafür

Nicht jede Folge besitzt einen Grenzwert.
So eine Folge heißt dann divergent.
BEISPIEL
Die Folge
![]() besitzt keinen Grenzwert, da sie größer als jede beliebige
natürliche Zahl wird.
besitzt keinen Grenzwert, da sie größer als jede beliebige
natürliche Zahl wird.
Diese Folge ,,strebt`` allerdings gegen ![]() .Derartige Folgen heißen bestimmt divergent
gegen
.Derartige Folgen heißen bestimmt divergent
gegen ![]() (bzw.
(bzw. ![]() ).
Wir schreiben dafür
).
Wir schreiben dafür

Folgen, die weder konvergent noch bestimmt divergent sind heißen ( unbestimmt) divergent.
BEISPIEL
Die Folge
![]() besitzt keinen Grenzwert. Der Grenzwert ist weder 1 oder
besitzt keinen Grenzwert. Der Grenzwert ist weder 1 oder ![]() , noch strebt die Folge gegen
, noch strebt die Folge gegen
![]() oder
oder ![]() . Sie ist daher (unbestimmt) divergent.
. Sie ist daher (unbestimmt) divergent.
Die Grenzwerte wichtiger Folgen.
| = | ||
| = | ![$\left\lbrace
\begin{array}[c]
{rl}
+\infty
\hiddenampersand
\mbox{für }\alp...
...ine
0
\hiddenampersand
\mbox{für }\alpha<0\hiddennewline
\end{array} \right.$](img670.gif) |
|
| = | ![$\left\{ \begin{array}[c]
{rl}
+\infty
\hiddenampersand
\mbox{für }q\gt 1\hidd...
...xists
\hiddenampersand
\mbox{für }q\leq{}-1\hiddennewline
\end{array} \right.$](img672.gif) |
|
| = | ||
| = | ||
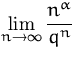 |
= | ![$\left\{ \begin{array}[c]
{rl}
0
\hiddenampersand
\mbox{für }\vert q\vert\gt 1...
...sts
\hiddenampersand
\mbox{für }0\gt q\gt-1\hiddennewline
\end{array} \right.$](img678.gif) |
Mit Hilfe von Rechenregeln lassen sich Grenzwerte komplexerer Folgen auf die Grenzwerte einfacherer (bekannter) Folgen zurückführen.
Im folgenden seien ![]() und
und ![]() konvergente
Folgen mit
konvergente
Folgen mit ![]() und
und
![]() .
. ![]() sei eine
beschränkte Folge.
sei eine
beschränkte Folge.
| REGEL | ||
| (1) | ||
| (2) | ||
| (3) | ||
| (4) | 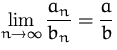 |
für |
| (5) | falls |
|
| (6) |
Ausdrücke der Form ![]() ,
, ![]() oder
oder
![]() sind nicht definiert.
Der Grenzwert könnte jeder beliebige Wert bzw. die Folge divergent sein.
Aus
sind nicht definiert.
Der Grenzwert könnte jeder beliebige Wert bzw. die Folge divergent sein.
Aus ![]() läßt sich nicht schließen, daß
läßt sich nicht schließen, daß
![]() (oder
(oder ![]() ).
).
BEISPIEL
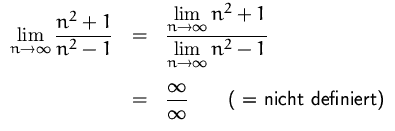
Trick: Kürzen durch die
höchste vorkommende Potenz im
Nenner.
![$
\begin{array}
{rcl}
{\displaystyle\lim\limits_{n\to\infty}\frac{n^2+1}{n^2-1...
...-n^{-2}}}\\ [4ex]
&=&
{\displaystyle\frac{1}{1}}\\ [2ex]
&=& 1
\end{array} $](img698.gif)