previous: Renten (nachschüssig) up: Folgen und Reihen next: Reelle Funktionen

Kredite  

In der  Tilgungsrechnung geht es um die Rückzahlung von Krediten, Darlehen udg. Im Falle gleichbleibender Rückzahlungsraten können wir zur Berechnung der Kreditrate die Rentenrechnung verwenden.

Wir setzen dabei den Barwert der Tilgungszahlungen gleich der ursprünglichen Kredithöhe $K$.

Sei im folgenden $X$ die Höhe der Tilgungsraten, $p$ der Zinsatz und $n$ die Laufzeit des Kredits, dann ist

$$K=B_n=X\cdot\frac{q^n-1}{q^n(q-1)}$$

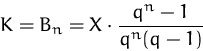
Daraus erhalten wir durch Umformen für die Höhe der Kreditrate

$\mbox{\ovalbox{$\displaystyle X=K\cdot q^n\frac{q-1}{q^n-1}$}}$

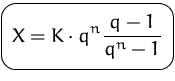
Falls die Kreditrate bekannt ist, können wir aus dieser Formel auch die die Laufzeit des Kredites berechnen:

$$K=X\frac{q^n-1}{q^n(q-1)}$$

Multiplizieren mit dem Nenner der rechten Seite

$$K q^n(q-1)=X(q^n-1)$$

Zusammenfassen aller Terme mit $q^n$

$$q^n(K(q-1)-X)+X=0$$

Isolieren von $n$ auf der linken Seite

$$q^n=\frac{-X}{K(q-1)-X}=\frac{X}{X-K(q-1)}$$

Logarithmieren

$$n \ln q= \ln\left(\frac{X}{X-K(q-1)}\right) =\ln X-\ln(x-K(q-1))$$

Division

$\mbox{\ovalbox{$\displaystyle n=\frac{\ln X-\ln(x-K(q-1))}{\ln q}$}}$

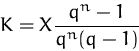
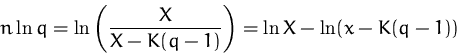
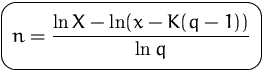
BEISPIEL
Ein Kredit über 100000 Geldeinheiten wird mit 8,5% p.a. verzinst.

(a) Wie hoch sind die jährlichen Tilgungszahlungen bei einer Laufzeit von 5 Jahren?

$K=100\,000$, $q=1{,}085$, $n=5$.

$$X=100\,000\cdot1{,}085^5\frac{1{,}085-1}{1{,}085^5-1}\approx 25\,376{,}58$$

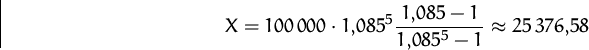
(b) Wie hoch muß die Laufzeit des Kredits angesetzt werden, damit die Rückzahlungsraten 15000 Geldeinheiten nicht übersteigen?

Für eine jährliche Tilgungszahlung von $X=15\,000$, $q=(1+p)=1{,}085$ und $K=100\,000$ erhalten wir

$$n=\frac{\ln 15\,000-\ln (15\,000-100\,000\cdot 0{,}085)}{\ln 1{,}085} \approx 10{,}25$$

Die Laufzeit muß daher mindestens 11 Jahre betragen.

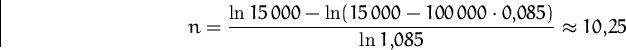
(Immer aufrunden!)