Sei ![]() eine
eine ![]() -Matrix.
Wir müssen die Gleichung
-Matrix.
Wir müssen die Gleichung
![]()
![]()
Dann ist ![]() aber kein Eigenwert.
aber kein Eigenwert.
![]() ist genau dann Eigenwert von
ist genau dann Eigenwert von ![]() , wenn
, wenn
![]() nicht invertierbar ist, d.h. wenn
nicht invertierbar ist, d.h. wenn
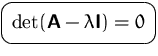
![]() ist ein Polynom
ist ein Polynom ![]() -ten Grades
und heißt das
charakteristische Polynom
der Matrix
-ten Grades
und heißt das
charakteristische Polynom
der Matrix ![]() .
.
Die Eigenwerte sind die Nullstellen dieses Polynoms.
BEISPIEL
Wir suchen die Eigenwerte von
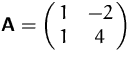 .
.
Dazu bilden wir das charakteristische Polynom und berechnen deren Nullstellen.
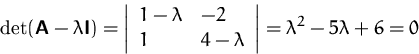
Die Lösungen dieser quadratischen Gleichung sind
![]()
![]() besitzt daher die Eigenwerte 2 und 3.
besitzt daher die Eigenwerte 2 und 3.
Es kann sein, daß alle Nullenstellen des charakteristischen Polynoms komplex sind. (komplexe Eigenwerte)