Wir führen ein neue Zahl ![]() ein, mit der Eigenschaft
ein, mit der Eigenschaft
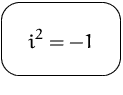
Die Zahlen der Form ![]() (z.B.
(z.B. ![]() ),
), ![]() heißen,
imaginäre Zahlen.
heißen,
imaginäre Zahlen.
Eigenschaften von ![]() :
:
Mit komplexen Zahlen kann wie gewohnt gerechnet
werden.
Für die Division gilt dabei:
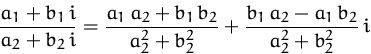
BEISPIEL
![]()
![]()
![]()
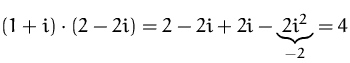
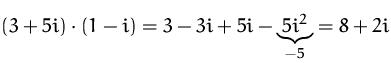
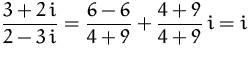
Wenn ![]() ein komplexe Lösung von
ein komplexe Lösung von
![]() ist,
dann auch
ist,
dann auch ![]() .
.
![]() heißt die zu
heißt die zu ![]() konjungiert komplexe Zahl.
konjungiert komplexe Zahl.