previous: Die inverse Matrix up: Die inverse Matrix next: Existenz der inversen Matrix

Was ist die inverse Matrix?  

Wir wollen den Produktionsvektor $\mathsfbf{x}$ durch den Nachfragevektor $\mathsfbf{b}$ ausdrücken.

Dazu müssen wir die Gleichung $\mathsfbf{b}=(\mathsfbf{I}-\mathsfbf{V})\,\mathsfbf{x}$nach $\mathsfbf{x}$ auflösen.

Wäre $(\mathsfbf{I}-\mathsfbf{V})$ eine reelle Zahl, könnten wir dies durch Division erreichen. Eine Division ist aber in der Matrixalgebra nicht definiert. Wir können aber unser Ziel durch Multiplikation mit der inversen Matrix erreichen.

 

DEFINITION (INVERSE MATRIX)
Falls für eine quadratische Matrix $\mathsfbf{A}$ eine Matrix $\mathsfbf{A}^{-1}$ mit der Eigenschaft

$\mbox{\ovalbox{$\displaystyle \mathsfbf{A}\cdot \mathsfbf{A}^{-1}=\mathsfbf{A}^{-1}\cdot \mathsfbf{A} = \mathsfbf{I}$}}$

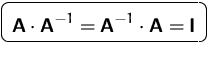
existiert, dann heißt $\mathsfbf{A}^{-1}$ die  inverse Matrix von $\mathsfbf{A}$.

Die Matrix $\mathsfbf{A}$ heißt  invertierbar falls sie eine Inverse besitzt. Andernfalls heißt sie  singulär.

Falls $(\mathsfbf{I}-\mathsfbf{V})^{-1}$ existiert, erhalten wir:

$$\begin{array} {rcl} \mathsfbf{b} &=&(\mathsfbf{I}-\mathsf... ...mathsfbf{V})^{-1}\cdot\mathsfbf{b} &=& \mathsfbf{x}\end{array}$$

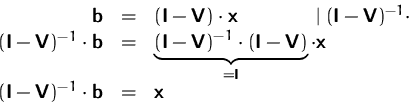
Achtung!

Die Multiplikation muß auf beiden Seiten der Gleichung von derselben Seite erfolgen!

Rechenregeln (vgl.) für die inverse Matrix:

 

$$\mathsfbf{A} \mathsfbf{B} \Rightarrow \mathsfbf{A}\cdot\mathsfbf{B}$$

$$(\mathsfbf{A}^{-1})^{-1} = \mathsfbf{A}$$

$$(\mathsfbf{A}\cdot \mathsfbf{B})^{-1} = \mathsfbf{B}^{-1}\cdot \mathsfbf{A}^{-1}$$

$$(\mathsfbf{A}^t)^{-1} = (\mathsfbf{A}^{-1})^t$$

Achtung!

Die inverse Matrix ist nur für quadratische Matrizen definiert.