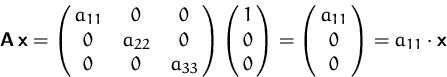Wir betrachten ein Leontief-Modell für eine Volkswirtschaft:
Wir betrachten ein Leontief-Modell
für eine Volkswirtschaft:
![]() sei die Produktion,
sei die Produktion, ![]() die Verbrauchsmatrix,
der Konsum innerhalb der Volkswirtschaft ist daher
die Verbrauchsmatrix,
der Konsum innerhalb der Volkswirtschaft ist daher
![]() .
Wenn der Konsum gleich der Produktion ist, d.h. wenn
.
Wenn der Konsum gleich der Produktion ist, d.h. wenn
![]()
Wir suchen nun nach einer Methode, um festzustellen, ob ein
Leontief-Modell geschlossen ist.
Es handelt sich dabei um Eigenwertproblem.
DEFINITION (EIGENWERT UND EIGENVEKTOR)
Ein Vektor ![]() ,
, ![]() , heißt Eigenvektor einer
, heißt Eigenvektor einer ![]() -Matrix
-Matrix
![]() zum Eigenwert
zum Eigenwert ![]() , falls
Die Eigenwerte der Matrix
, falls
Die Eigenwerte der Matrix 
![]() sind alle
sind alle ![]() für die ein Eigenvektor existiert.
für die ein Eigenvektor existiert.
BEISPIEL
Sei ![]() eine Diagonalmatrix im
eine Diagonalmatrix im ![]() und
und
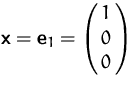 ein Einheitsvektor. Dann ist
ein Einheitsvektor. Dann ist