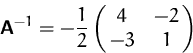Wir wollen die Inverse einer Matrix
![]() mit Hilfe der Determinante ausrechnen.
mit Hilfe der Determinante ausrechnen.
Sei ![]() ,wobei
,wobei ![]() die
Streichungsmatrix
ist.
Die Zahl
die
Streichungsmatrix
ist.
Die Zahl ![]() heißt Kofaktor von
heißt Kofaktor von ![]() .
.
Wir können diese Kofaktoren in einer Matrix
zusammenfassen ( Kofaktorenmatrix) und transponieren.
Wir erhalten dadurch die adjungierte Matrix
![]() von
von ![]() .
.

Wie sieht das Produkt ![]() aus?
aus?
Das Produkt aus ![]() -ter Zeile von
-ter Zeile von ![]() und
und ![]() -ter
Spalte von
-ter
Spalte von ![]() ist
nach dem Entwicklungssatz
(Entwicklung nach einer Spalte)
ist
nach dem Entwicklungssatz
(Entwicklung nach einer Spalte)
![\begin{displaymath}
\begin{array}
{rcl}
\sum_{i=1}^n a_{ij}\cdot A_{ik}
&=&
\...
...kebox[0pt]{$k$-te Spalte}},
\ldots, \mathsfbf{a}_n)\end{array}\end{displaymath}](img491.gif)
Die ![]() sind die einzelnen Spaltenvektoren von
sind die einzelnen Spaltenvektoren von ![]() .
.
Falls ![]() , dann ist dieses Produkt gerade
, dann ist dieses Produkt gerade ![]() .
.
Andernfalls ist dieses Produkt gleich 0 (zwei Spalten der Determinante gleich).
![]()
Für die Inverse erhalten wir
BEISPIEL
Gesucht ist die Inverse von
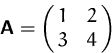
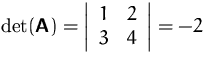
![]() ,
, ![]() ,
, ![]() und
und ![]()
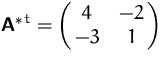
Daher: