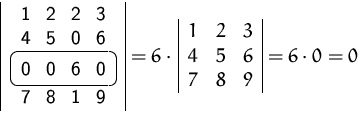Determinanten von
Determinanten von
![]() -Matrizen lassen sich durch den
Laplace'schen Entwicklungssatz
rekursiv berechnen.
-Matrizen lassen sich durch den
Laplace'schen Entwicklungssatz
rekursiv berechnen.
Entwicklung nach der ![]() -ten Spalte bzw.
-ten Spalte bzw. ![]() -ten Zeile:
-ten Zeile:
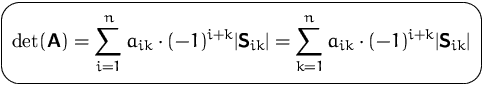
![]() ist die
ist die ![]() -Matrix,
die man erhält, wenn die
-Matrix,
die man erhält, wenn die ![]() -te Zeile und
-te Zeile und ![]() -te Spalte gestrichen
wird
( ,,Streichungsmatrix``).
-te Spalte gestrichen
wird
( ,,Streichungsmatrix``).
Es ist dabei völlig egal, nach welcher Zeile oder Spalte entwickelt wird.
BEISPIEL
Wir berechnen die Determinante von
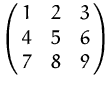
Entwicklung nach der ersten Zeile:
![\begin{displaymath}
\begin{array}
{rcl}
\setlength {\fboxsep}{2mm}
\begin{arr...
... (-3) - 2\cdot (-6) + 3\cdot (-3)\\ [1ex]
& = & 0
\end{array}\end{displaymath}](img480.gif)
Wir können aber auch nach der zweiten Spalte entwickeln:
![\begin{displaymath}
\begin{array}
{rcl}
\setlength {\fboxsep}{2mm}
\begin{arr...
...(-6) + 5\cdot (-12) -8 \cdot (-6)\\ [1ex]
& = & 0
\end{array}\end{displaymath}](img481.gif)
Wir wählen stets stets eine Zeile oder Spalte, die möglichst viele Nullen enthält.
BEISPIEL