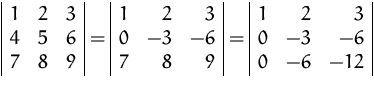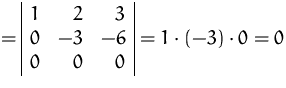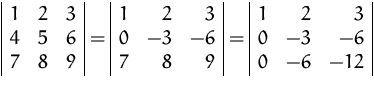
Benützen die Eigenschaft
(6)
der Determinante um die Matrix
in eine Dreiecksmatrix umzuformen. Die Determinante ist dann
das Produkt der Diagonalelemente der Dreiecksmatrix
(9).
Das Verfahren ist ähnlich dem
Gaußschen Eliminationsverfahren. Das Vertauschen von zwei Zeilen
(4)
oder das Multiplizieren einer Zeile mit einer Zahl
(1b)
ist nun aber nicht erlaubt bzw. verändert den Wert der Determinante.
BEISPIEL