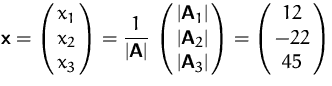eines linearen Gleichungssystems in
Die Cramersche Regel ist eine Methode die Lösung
eines linearen Gleichungssystems in ![]() Gleichungen und
Gleichungen und ![]() Unbekannten zu finden, sofern die Lösung existiert und eindeutig ist.
Unbekannten zu finden, sofern die Lösung existiert und eindeutig ist.
![]()
Falls ![]() regulär ist (
regulär ist (![]() ),
dann gilt
),
dann gilt
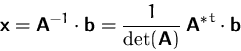
Wir erhalten daher für ![]()
![\begin{displaymath}
\begin{array}
{rcl}
x_k
&=&
\frac{1}{\det(\mathsfbf{A})} ...
...kebox[0pt]{$k$-te Spalte}},
\ldots, \mathsfbf{a}_n)\end{array}\end{displaymath}](img505.gif)
Sei nun ![]() die Matrix, die wir aus
die Matrix, die wir aus ![]() erhalten,
wenn wir die
erhalten,
wenn wir die ![]() -te Spalte durch den Vektor
-te Spalte durch den Vektor ![]() ersetzen.
ersetzen.
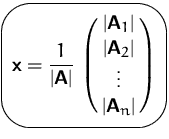
Dann ist die Lösung von
![]() gleich
gleich
Dieses Verfahren eignet sich nur, wenn ![]() eine reguläre
quadratische Matrix ist!!
eine reguläre
quadratische Matrix ist!!
(Eine Methode die hingegen immer funktioniert ist z.B. das
Gaußsche Eliminationsverfahren.)
BEISPIEL
Gesucht ist die Lösung von
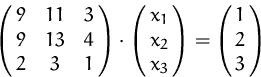
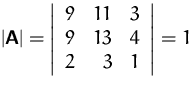
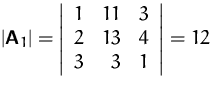
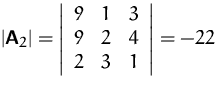
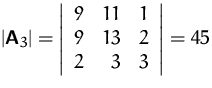
Lösung: