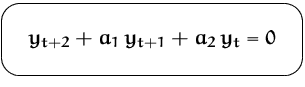
![]()
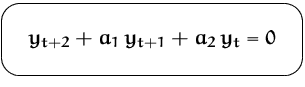
Analog zu linearen DG machen wir den Ansatz
![]()
![]()
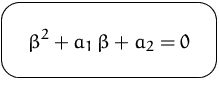
mit den Lösungen
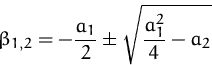
Fall: 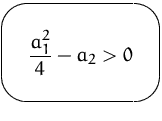
![]() sind reell (zwei reelle Lösungen)
sind reell (zwei reelle Lösungen)
Die allgemeine Lösung lautet
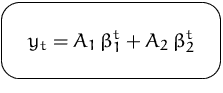
Der Ansatz ![]() führt zur
Charakteristischen Gleichung
führt zur
Charakteristischen Gleichung
![]()
Allgemeine Lösung:
![]()
Fall: 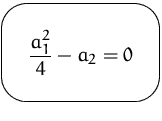
![]() ist reell (eine doppelte reelle Nullstelle)
ist reell (eine doppelte reelle Nullstelle)
Analog zur Differentialgleichung erhalten wir die allgemeine Lösung
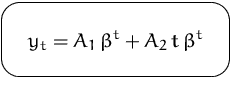
BEISPIEL
Lösung von
![]() .
.
Aus der charakteristischen Gleichung
![]()
Die allgemeine Lösung lautet daher
![]()
Fall: 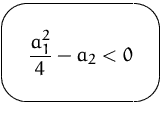
![]() sind komplex
sind komplex
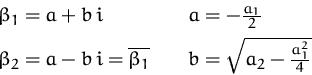
In Polarkoordinaten:
![]()
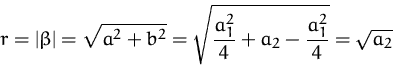
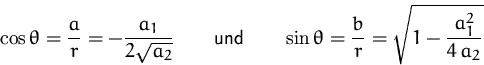
Daraus erhalten wir die (reellen) Lösungen:
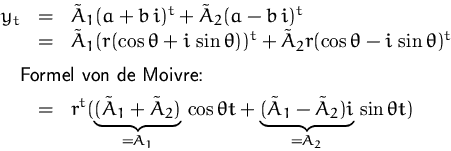
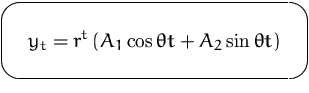
Aus der charakteristischen Gleichung erhalten wir
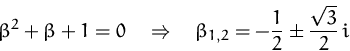
Polarkoordinaten:
![]() ,
, ![]() (da
(da ![]() und
und
![]() ).
).
Die allgemeine Lösung lautet daher
![]()