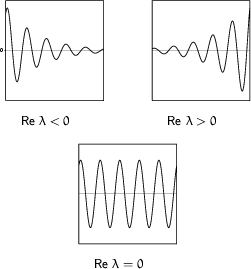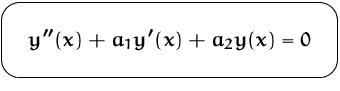
![]()
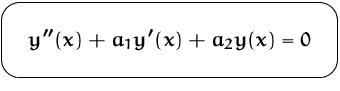
Ansatz: ![]()
Ableitungen:
![]()
![]()
Diese Gleichung wird erfüllt genau dann, wenn
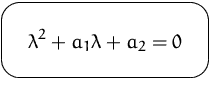
Diese Gleichung heißt
charakteristische Gleichung.
LöSUNG:
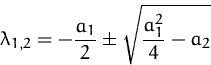
Fall: 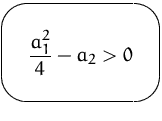
![]() sind reell (zwei reelle Lösungen).
sind reell (zwei reelle Lösungen).
![]()
sind Lösungen, und damit auch ihre Summe:
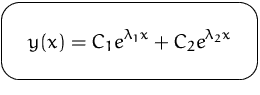
BEISPIEL
Lösung von ![]()
Der Ansatz ![]() führt zur charakteristischen
führt zur charakteristischen
Gleichung
![]()
![]()
allgemeine Lösung:
![]()
Fall: 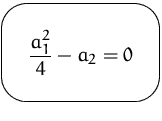
![]() ist reell (doppelte Nullstelle)
ist reell (doppelte Nullstelle)
![]()
Zweite Lösung: ![]()
Zeigen: ![]() ist Lösung
ist Lösung
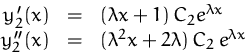
![]() und
und
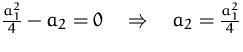
![]()
![$\quad
=[(\frac {a_1^2}{4} x - a_1) + a_1 (-\frac {a_1}{2} x + 1)
+ \frac{a_1^2}{4} x ]C_2\,e^{\lambda x}$](img1784.gif)
![$\quad
=[\frac{a_1^2}{4}x-a_1-\frac{a_1^2}{2}x+a_1+\frac{a_1^2}{4}x]
C_2\,e^{\lambda x} = 0
$](img1785.gif)
ALLGEMEINE LöSUNG:
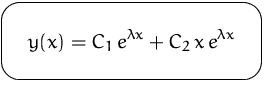
BEISPIEL
Lösung von ![]()
charakteristische Gleichung:
![]()
![]()
Fall: 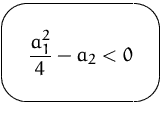
![]() sind komplex
sind komplex
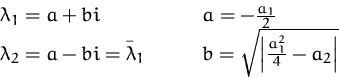
Lösungen:
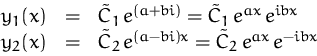
Reelle Lösungen:
![\begin{displaymath}
\begin{array}
{rcl}
y(x) & = & y_1 (x) + y_2 (x) \\ &=& \t...
...derbrace{(\tilde{C}_1-\tilde{C}_2)i}_{=C_2}\sin(bx)]\end{array}\end{displaymath}](img1793.gif)
ALLGEMEINE LöSUNG:
![$\mbox{\ovalbox{$\displaystyle y(x)= e^{ax}\cdot[ C_1 \cos(bx) + C_2 \sin(bx)]$}}$](img1794.gif)
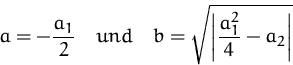
BEISPIEL
![]()
charakteristische Gleichung:
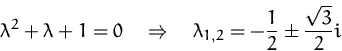
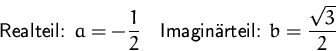
allgemeine Lösung:
![\begin{displaymath}
y(x) = e^{-\frac{1}{2}x} [C_1 \cos \frac{\sqrt{3}}{2} x + C_2 \sin
\frac{\sqrt{3}}{2} x]
\end{displaymath}](img1799.gif)
Oszillierende Lösungen der homogenen linearen DG: