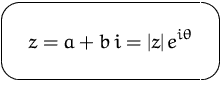Jeder komplexer Zahl ![]() wird ein Punkt
wird ein Punkt ![]() in der
Ebene zugordnet.
in der
Ebene zugordnet.
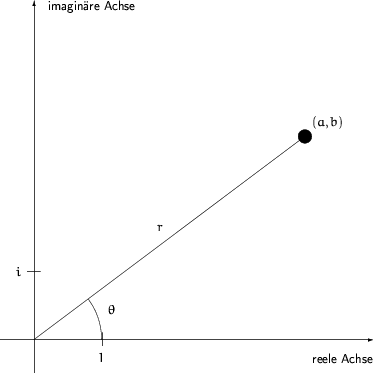
![]() kann auch durch den Abstand
kann auch durch den Abstand ![]() dieses Punktes vom Ursprung und dem Winkel
dieses Punktes vom Ursprung und dem Winkel ![]() festgelegt werden.
festgelegt werden.
![]()
![]() kartesische Koordinaten,
kartesische Koordinaten,
![]()
![]() Polarkoordinaten
Polarkoordinaten
der komplexen Zahl ![]() .
.
Es gilt
![]()
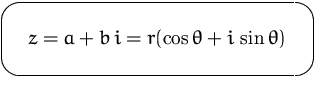
Der Abstand ![]() vom Ursprung heißt der
Absolutbetrag von
vom Ursprung heißt der
Absolutbetrag von ![]() und wird mit
und wird mit ![]() bezeichnet.
bezeichnet.
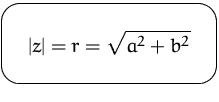
Multiplikation und Division ist in dieser Darstellung:
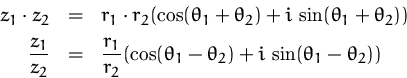
Potenzen durch die Formel von de Moivre:
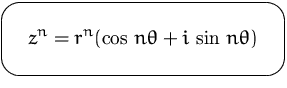
Es gilt folgende wichtige Relation: ( Eulersche Formel)
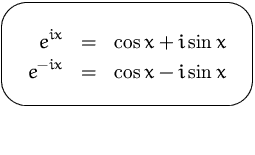
(Beweis durch Einsetzen in Taylorreihe)
Außerdem