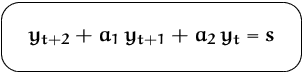
![]()
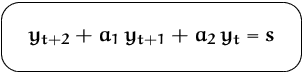
Die allgemeine Lösung läßt sich darstellen als
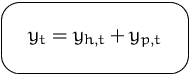
wobei
![]() ...
allgemeine Lösung der homogenen Glg. (
...
allgemeine Lösung der homogenen Glg. (![]() )
)
![]() ...
partikuläre Lösung der inhomogenen Gleichung
...
partikuläre Lösung der inhomogenen Gleichung
konstante Lösung: ![]()
![]()
![]()
Falls ![]() versuchen wir
versuchen wir ![]() :
:
![]()
![]()
![]()
![]()
BEISPIEL
Lösung der Differenzgleichung
![]() .
.
Die allgemeine Lösung der homogenen Differenzengleichung
(Beispiel):
![]()
partikuläre Lösung:
![]()
allgemeine Lösung der Differenzengleichung:
![]()
BEISPIEL
Lösung der Differenzengleichung
![]()
Die allgemeine Lösung der homogenen Differenzengleichung
(Beispiel):
![]()
partikuläre Lösung:
![]()
allgemeine Lösung der Differenzengleichung:
![]()