Was passiert mit dem Funktionswert einer Funktion ![]() , wenn das
Argument
, wenn das
Argument ![]() gegen einen bestimmten Wert
gegen einen bestimmten Wert ![]() strebt?
strebt?
DEFINITION (LIMES)
Wenn für jede Folge von Argumenten
![]() die Folge der Funktionswerte
die Folge der Funktionswerte
![]() gegen eine Zahl
gegen eine Zahl ![]() konvergiert, so heißt
konvergiert, so heißt
![]() der Grenzwert (oder Limes) der Funktion
der Grenzwert (oder Limes) der Funktion ![]() an der Stelle
an der Stelle ![]() . Wir schreiben dafür
. Wir schreiben dafür
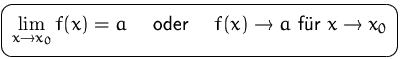
![]() muß nicht in der Definitionsmenge liegen und kann daher auch
muß nicht in der Definitionsmenge liegen und kann daher auch
![]() sein. Genauso muß
sein. Genauso muß ![]() nicht in der Wertemenge der Funktion liegen.
nicht in der Wertemenge der Funktion liegen.
Für Limiten von Funktionen gelten analoge Rechenregeln wie für Grenzewerte von Folgen.
Natürlich können wir nicht jede Folge von Argumenten untersuchen. Für einfache Funktionen eignet sich aber folgende Vorgangsweise:
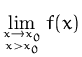 .
.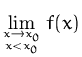 .
.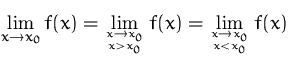 .
.
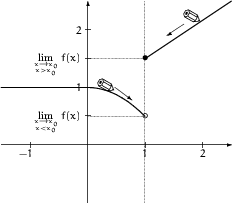
![]()
![]()
d.h., der Grenzwert an der Stelle ![]() existiert nicht.
existiert nicht.
Der Grenzwert ![]() existiert hingegen.
existiert hingegen.