previous: Graphen
up: Reelle Funktionen
next: Grenzwert einer Funktion
Ist 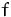 Injektiv?
Injektiv?
Unsere
Aufgabe ist es festzustellen, wieviele
Urbilder jedes 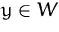 besitzt.
Dazu eignet sich der ,,Horizontalen-Test``.
besitzt.
Dazu eignet sich der ,,Horizontalen-Test``.
- (1)
- Wir zeichnen den Graphen der zu untersuchenden Funktion.
- (2)
- Wir zeichnen ein
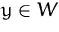 auf der
auf der 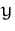 -Achse ein und legen eine
Gerade parallel zur
-Achse ein und legen eine
Gerade parallel zur 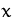 -Achse (Horizontale) durch diesen
-Achse (Horizontale) durch diesen 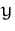 -Wert.
-Wert.
- (3)
- Die Anzahl der Schnittpunkte von Horizontale und Graph ist die
Anzahl der Urbilder von
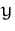 .
. - (4)
- Wir wiederholen (2) und (3) für eine repräsentative
Auswahl von
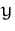 -Werten.
-Werten.
- (5)
- Interpretation:
Schneidet jede Horizontale den Graphen in
- (a)
- höchstens einem Punkt, so ist
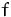 injektiv;
injektiv;
- (b)
- mindestens einem Punkt, so ist
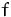 surjektiv;
surjektiv;
- (c)
- genau einem Punkt, so ist
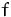 bijektiv.
bijektiv.
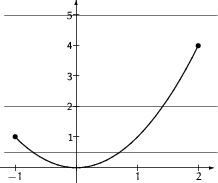
BEISPIEL
Die Funktion ![$f\colon [\,-1,2\,]\to {\mathbb R},\,x\mapsto x^2$](img881.gif) ist weder injektiv und noch surjektiv.
ist weder injektiv und noch surjektiv.
ACHTUNG:
Definitions- und Wertemenge sind Bestandteil der Funktion.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]() besitzt.
Dazu eignet sich der ,,Horizontalen-Test``.
besitzt.
Dazu eignet sich der ,,Horizontalen-Test``.
![]() ist weder injektiv und noch surjektiv.
ist weder injektiv und noch surjektiv.