Der Rang
DEFINITION (RANG EINER MATRIX)
Der Rang ![]() einer Matrix
einer Matrix
![]() ist die maximale Anzahl an linear unabhängigen Spalten.
ist die maximale Anzahl an linear unabhängigen Spalten.
Analog ist der Zeilenrang einer Matrix ![]() definieren als die maximale Anzahl an linear unabhängigen Zeilen
dieser Matrix. (Spalten-)Rang und Zeilenrang einer Matrix sind aber
immer gleich.
definieren als die maximale Anzahl an linear unabhängigen Zeilen
dieser Matrix. (Spalten-)Rang und Zeilenrang einer Matrix sind aber
immer gleich.
Berechnung des Ranges:
| (1) | Wir bringen die Matrix mit den Umformungsschritten des Gaußschen Eliminationsverfahrens in die Staffelform. |
| (2) | Die Anzahl der von Null verschiedenen Zeilen ergibt den Rang der Matrix. |
BEISPIEL
Die Matrizen aus obigen zwei Beispielen haben Rang 3
(![]() )
bzw. Rang 2
(
)
bzw. Rang 2
(![]() ).
).
Es gilt folgende Rechenregel:
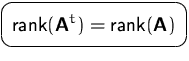
Der Rang einer ![]() -Matrix ist immer
-Matrix ist immer ![]() .
.
DEFINITION (REGULäRE MATRIX)
Eine ![]() -Matrix heißt regulär, falls sie
vollen Rang hat, d.h. falls
-Matrix heißt regulär, falls sie
vollen Rang hat, d.h. falls ![]() .
.