previous: Norm und inneres Produkt up: Matrizen und Vektoren next: Vorteile

Matrixdarstellung  

Leontief-Modell ( FORTSETZUNG)

Durch die Variablen $x_1$, $x_2$ und $x_3$ wird die Produktion der drei städtischen Betriebe beschrieben. Wir können diese drei Variablen in einen  Vektor zusammenfassen und mit einem eigenen Symbol versehen:

$\mbox{\ovalbox{$\displaystyle \mathsfbf{x} = \left( \begin{array} {c}x_1\\ x_2\\ x_3\\ \end{array} \right)$}}$

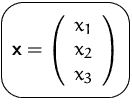
Ebenso können wir die Nachfrage durch einen Vektor $\mathsfbf{b}$und den internen Verbrauch durch einen Vektor $\mathsfbf{y}$ beschreiben.

$$\mathsfbf{y} = \left( \begin{array} {c}y_1\\ y_2\\ y_3\\ \... ...,1\,x_3\\ 0,0\,x_1&+&0,5\,x_2&+&0,1\,x_3\\ \end{array}\right)$$

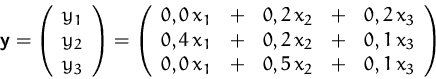
Mit Hilfe von Matrizenrechnung können wir $\mathsfbf{y}$ auch darstellen als

$$\mathsfbf{y}= \underbrace{\left( \begin{array} {ccc} 0,0&0,... ...left( \begin{array} {c} x_1\\ x_2\\ x_3\\ \end{array}\right)$$

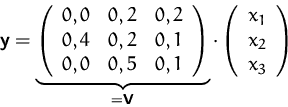
oder kurz als

$$\mathsfbf{y} = \mathsfbf{V}\cdot\mathsfbf{x}$$

Für die Nachfrage erhalten wir:

$$\mathsfbf{b} = \mathsfbf{x} - \mathsfbf{V}\cdot\mathsfbf{x} ... ...f{V}\cdot\mathsfbf{x} = (\mathsfbf{I}-\mathsfbf{V})\mathsfbf{x}$$