Eine Abbildung
Der Begriff der Abbildung oder Funktion ist einer der wichtigsten Begriffe in der Mathematik. Dabei wird jedem Element einer Definitionsmenge ein Merkmal (ein Element aus der Menge der zulässigen Merkmale, der sogenannten Wertemenge) eindeutig zugeordnet.
DEFINITION (ABBILDUNG)
Eine Abbildung ![]() ist definiert durch
Wir schreiben dafür
ist definiert durch
Wir schreiben dafür
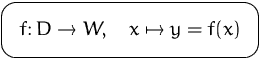
![]() ist das Argument (die unabhängige Variable)
von
ist das Argument (die unabhängige Variable)
von ![]() , der Ausdruck
, der Ausdruck ![]() der Funktionsterm der Abbildung
der Funktionsterm der Abbildung
![]() .
.
![]() heißt das Bild
(der Funktionswert) von
heißt das Bild
(der Funktionswert) von ![]() ,
,
![]() das Urbild von
das Urbild von ![]() .
.
BEISPIEL
![]() ,
,
![]() ,
,
![]()
,,Jedem Menschen wird sein Geburtstag zugeordnet`` ist eine Abbildung.
BEISPIEL
![]() ,
,
![]() ,
,
![]()
,,Jedem Menschen wird seine Staatsbürgerschaft zugeordnet`` ist keine Abbildung, da die Zuordnung nicht immer eindeutig (Doppelstaatsbürgerschaft) oder möglich (Staatenlose) ist.
Jedes Argument besitzt immer genau ein Bild. Die Anzahl der
Urbilder eines Elementes ![]() kann jedoch beliebig sein. Wir können
daher Funktionen nach der Anzahl der Urbilder einteilen.
kann jedoch beliebig sein. Wir können
daher Funktionen nach der Anzahl der Urbilder einteilen.
DEFINITION (INJEKTIV)
Die Einheitsfunktion oder identische Funktion: bildet das Argument auf sich selbst ab, d.h.
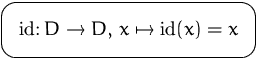
Ist eine Abbildung ![]() bijektiv, so können wir jedem
bijektiv, so können wir jedem
![]() sein Urbild
sein Urbild ![]() (d.h.
(d.h. ![]() ) zuordnen.
Wir erhalten dadurch wieder eine Abbildung
) zuordnen.
Wir erhalten dadurch wieder eine Abbildung ![]() mit der Definitionsmenge
mit der Definitionsmenge ![]() und der Wertemenge
und der Wertemenge ![]() :
:
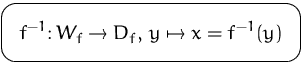
Diese Abbildung heißt
Umkehrfunktion
oder inverse Abbildung.
Sie hat die Eigenschaft, daß für alle Elemente ![]() und
und ![]() gilt:
gilt:
![]()