previous: Rang einer Matrix up: Matrizen und Vektoren next: Die inverse Matrix

Die erweitere Koeffizientenmatrix  

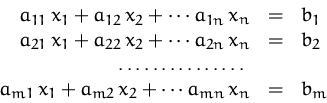
Wir können jedes lineare Gleichungssystem

$$\begin{array} {rcl} a_{11}\,x_1 + a_{12}\,x_2 + \cdots a_{1... ...}\,x_1 + a_{m2}\,x_2 + \cdots a_{mn}\,x_n &=& b_m\\ \end{array}$$

in Matrixform anschreiben:

$$\mathsfbf{A}\cdot\mathsfbf{x}=\mathsfbf{b}$$

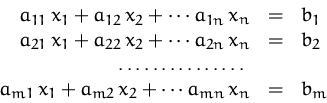
wobei die Matrix $\mathsfbf{A}=(a_{ij})$ als  Koeffizientenmatrix des Gleichungssystems bezeichnet wird.

Beim Gaußschen Eliminationsverfahren haben wir die Koeffizienten $\mathsfbf{A}$ und die Konstanten $\mathsfbf{b}$ zu einer Matrix $(\mathsfbf{A},\mathsfbf{b})$, der sognannten  erweiterten Koeffizientenmatrix zusammengefaßt.

Mit Hilfe der Ränge dieser beiden Matrizen können wir nun feststellen, wieviele Lösungen das lineare Gleichungssystem besitzt.

 

$$\bullet$$ Das Gleichungssystem hat genau eine Lösung, falls

$$\mbox{rank}(\mathsfbf{A}) = \mbox{rank}(\mathsfbf{A},\mathsfbf{b}) = n$$

$$\bullet$$ Das Gleichungssystem hat unendlich viele Lösungen, falls

$$\mbox{rank}(\mathsfbf{A}) = \mbox{rank}(\mathsfbf{A},\mathsfbf{b})<n$$

$$\bullet$$ Das Gleichungssystem ist inkonsistent, falls

$$\mbox{rank}(\mathsfbf{A}) < \mbox{rank}(\mathsfbf{A},\mathsfbf{b})$$

BEISPIEL
Koeffizientenmatrix und erweiterte Koeffizientenmatrix des Gleichungssystems

$$\begin{array} {rcrcrcr} 3\,x_1 &+& 4\,x_2 &+& 5\,x_3 &=& 1\... ...x_3 &=& 2\\ 5\,x_1 &+& 6\,x_2 &+& 3\,x_3 &=& 4\\ \end{array}$$

lauten

$\mathsfbf{A} = \left( \begin{array} {rrr} 3 &4 &5 \\ 1 & 1&-1 \\ 5 &6 &... ...array} {rrrr} 3 &4 &5 &1\\ 1 & 1&-1 &2\\ 5 &6 & 3&4\\ \end{array} \right)$

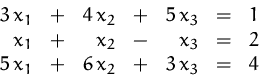
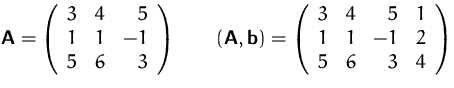
Umformung der erweiterten Koeffizientenmatrix in die Staffelform ergibt

$$\left( \begin{array} {rrrr} 3 & 4 & 5 & 1\\ 0 & -1 & -8 & 5\\ 0 & 0 & 0 & -3\\ \end{array} \right)$$

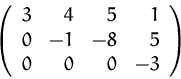
$\mbox{rank}(\mathsfbf{A}) = 2 <\mbox{rank}(\mathsfbf{A},\mathsfbf{b})=3$, d.h. das Gleichungssystem ist inkonsistent.