previous: Homogene lineare Differenzengleichungen up: Differenzengleichungen erster Ordnung next: Ein Cobweb-Model

Inhomogene lineare Differenzengleichungen  

$\bullet\quad$$\mbox{\ovalbox{$\displaystyle y_{t+1}+a\,y_t = s$}}$

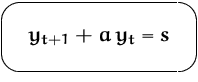
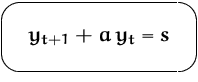
Die allgemeine Lösung läßt sich stets in der Gestalt

$$y_t = y_{h,t} + y_{p,t}$$

darstellen, wobei

$y_{h,t}$ ... allgemeine Lösung der homogenen Glg. ($s=0$)
$y_{p,t}$ ... partikuläre Lösung der inhomogenen Gleichung

Wie findet wir $y_{p,t}$?

Konstante Lösung: $y_{p,t}=c$

$$y_{p,t} + a\,y_{,t}p = c + a\,c = s$$

$$\quad\Rightarrow\quad y_{p,t} = c = \frac{s}{1+a} \quad\mbox{falls $a\not= -1$}$$

Falls $a=-1$ versuchen wir $y_{p,t}=c\,t$:

$$c\,(t+1) + (-1)\,c\,t = s \quad\Rightarrow\quad c = \frac{s}{(t+1)-t} = s$$

$$\quad\Rightarrow\quad y_{p,t}=s\,t$$

Allgemeine Lösung:

$\mbox{\ovalbox{$\displaystyle y_t = \left\{ \begin{array} {ll} A\,(-a)^t + \di... ...2ex] A\,(-a)^t + s\,t = A + s\,t & \mbox{falls } a = -1 \end{array}\right.$}}$

Lösung des Anfangswertproblems durch Einsetzen.

BEISPIEL
Lösung von $y_{t+1}-2\,y_t=2$ mit $y_0=1$:

Allgemeine Lösung: (da $a=-2\not=-1$)

$$y_t = A\,(-(-2))^t + \frac{2}{1-2} = A\,2^t - 2,$$

Lösung des Anfangswertproblems durch Einsetzen:

$$1 = y_0 = A\,2^0 - 2 \quad\Rightarrow\quad A = 3 \quad\Rightarrow\quad y_t = 3\cdot 2^t - 2$$

Das Verhalten der Lösung hängt genauso vom Parameter $a$ ab wie im Fall der homogenen linearen Differenzengleichung (vgl.).

BEISPIEL
Lösung von $y_{t+1}-\,y_t=3$ mit $y_0=4$:

Allgemeine Lösung: (da $a=-1$)

$$y_t = A\, + 3\,t$$

Lösung des Anfangswertproblems durch Einsetzen:

$$4 = y_0 = A + 3\cdot 0 \quad\Rightarrow\quad A = 4 \quad\Rightarrow\quad y_t = 4 + 3\,t$$

BEISPIEL
  Wollen in unserem einfachen Marktmodell diskrete Zeit einführen:

$$\begin{array} {ll} q_{d,t} = \alpha - \beta p_t\quad & (\al... ...1} = p_t + j (q_{d,t} - q_{s,t})\quad & (j \gt 0) \end{array}$$

$$q_{d,t}$$ ... Nachfrage,

$$q_{s,t}$$ ... Angebot und

$$p_t t$$ ...

Angebot und Nachfrage hängen vom Preis der entsprechenden Periode ab, der Preis ist eine Funktion von Preis, Angebot und Nachfrage der vorhergehenden Periode.

Einsetzen von Nachfrage- und Angebotsfunktion in die dritte Gleichung ergibt eine inhomogene lineare Differenzengleichung erster Ordnung:

$$p_{t+1} + (j (\beta+\gamma)-1)\,p_t = j(\alpha + \gamma)$$

Da alle Konstanten größer Null sind, ist $j (\beta+\gamma)-1\not=-1$ und wir erhalten die allgemeine Lösung

$$p_t = A\,(1-j(\beta+\delta))^t + \frac{\alpha+\gamma}{\beta+\delta} = A\,(1-j(\beta+\delta))^t + \bar{p}$$

wobei $\bar{p}=\frac{\alpha+\gamma}{\beta+\delta}$ der Preis im Marktgleichgewicht ist.

Durch Einsetzen der Anfangsbedingung erhalten wir die Lösung

$$p_t = (p_0 - \bar{p}) (1-j(\beta+\delta))^t + \bar{p}$$