previous: Iteration up: Differenzengleichungen erster Ordnung next: Inhomogene lineare Differenzengleichungen

Homogene lineare Differenzengleichungen  

$\bullet\quad$$\mbox{\ovalbox{$\displaystyle y_{t+1}+a\,y_t = 0$}}$

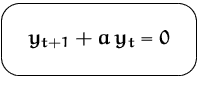
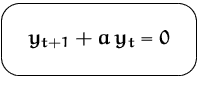
Vermuten wegen des obigen Beispiels:

$$y_t = A\,\beta^t, \quad A\,\beta\not=0,$$

wobei $A$ eine reelle Zahl ist (allgemeine Lösung).

Die Differenzengleichung muß für alle $t$ gelten:

$$y_{t+1}+a\,y_t = A\,\beta^{t+1} + a\, A\,\beta^t = 0.$$

Division durch $A\,\beta^t$ ergibt $\beta+a = 0$ und somit $\beta=-a$.

$\mbox{\ovalbox{$\displaystyle y_t = A\,(-a)^t$}}$

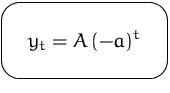
Verhalten der Lösung hängt vom Parameter $a$ ab.

Es gibt sieben Bereiche für $a$(Abbildung), die sich kurz beschreiben lassen mit

$$\Leftrightarrow a\gt$$ oszillierend

$$\Leftrightarrow \vert a\vert<1$$ konvergent