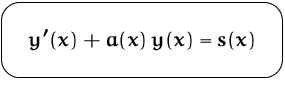
![]()
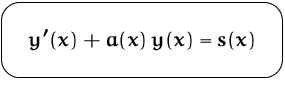
Die Lösung
läßt sich stets in der Gestalt
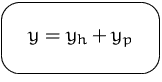
darstellen, wobei
![]() ... allgemeine Lösung der homogenen DG (
... allgemeine Lösung der homogenen DG (![]() )
)
![]() ... partikuläre Lösung der inhomogenen DG
... partikuläre Lösung der inhomogenen DG
Wie findet man ![]() ?
?
1.
Falls ![]() und
und ![]() Konstante sind, dann
setzen wir
Konstante sind, dann
setzen wir ![]() .
.
BEISPIEL
Lösung von ![]()
![]()
![]()
![]()
2. Methode der Variation der Konstanten
Ersetzen in der allgemeinen Lösung der homogenen DG die Konstante ![]() durch eine Funktion
durch eine Funktion ![]() :
:
![]()
Differenzieren
![]()
BEISPIEL
Lösung von
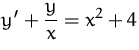
allgemeine Lösung der homogenen DG: ![]()
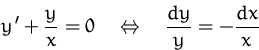
![]()
![]()
partikuläre Lösung: (Variation der Konstanten)
![]()
![]()
![]()
![]()
Integrieren:
![]()
![]()
Allgemeine Lösung der inhomogenen DG:
![]()
Probe: ![]()
![]()
Die partikuläre Lösung der inhomogene DG is eine spezielle Lösung und enthält daher keine Integrationskonstante.
BEISPIEL EINFACHES MARKTMODELL
Für eine bestimmte Ware gelten folgende Nachfrage- und Angebotsfunktionen:
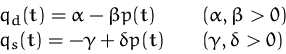
Die Preisänderung ![]() soll proportional zur Differenz von
Nachfrage und Angebot sein:
soll proportional zur Differenz von
Nachfrage und Angebot sein:
![]()
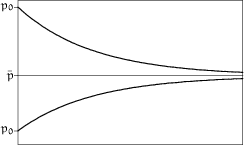
Wie verhält sich der Preis ![]() im Laufe der Zeit
im Laufe der Zeit ![]() ?
?
Im Marktgleichgewicht gilt:
![]()
Aus der Preisänderung erhalten wir
![]()
eine inhomogene lineare DG erster Ordnung
![]()
LöSUNG:
homogene DG:
![]()
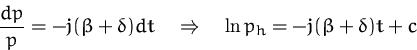
![]()
partikuläre Lösung:
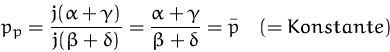
allgemeine Lösung:
![]()
Lösung des Anfangswertproblems mit ![]()
![]()
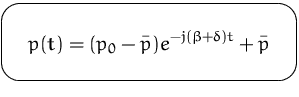
![]() für
für ![]() unabhängig von
unabhängig von ![]()