previous: Inhomogene lineare Differenzengleichungen up: Differenzengleichungen erster Ordnung next: Differenzengleichungen zweiter Ordnung

Ein Cobweb-Model  

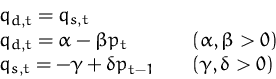
Betrachten folgendes Marktmodell:

$$\begin{array} {ll} q_{d,t} = q_{s,t} & \\ q_{d,t} = \alpha... ...\gamma +\delta p_{t-1}\quad & (\gamma, \delta \gt 0)\end{array}$$

In jeder Periode herrscht Marktgleichgewicht. Das Angebot hängt vom Preis der vorhergehenden Periode ab.

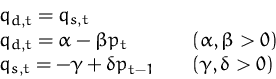
Einsetzen der zweiten und dritten Gleichung in die erste ergibt die inhomogene lineare Differenzengleichung

$$\textstyle \beta\,p_t + \delta\,p_{t-1} = \alpha + \gamma \q... ...+1} + \frac{\delta}{\beta}\,p_t = \frac{\alpha + \gamma}{\beta}$$

mit der Lösung

$$p_t = (p_0-\bar{p})\left(-\frac{\delta}{\beta}\right)^t + \bar{p}$$

wobei $\bar{p}=\frac{\alpha+\gamma}{\beta+\delta}$.

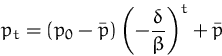
Da alle Konstanten positiv sind, oszilliert die Lösung immer. Sie konvergiert genau dann gegen $\bar{p}$, wenn $\left\vert\frac{\delta}{\beta}\right\vert<1$.

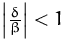Können das Modell auch graphisch analysieren:

$$q_{d,t} = q_{s,t}, \quad q_{d,t} = D(p_t), \quad q_{s,t} = S(p_{t-1})$$

Wir zeichnen Angebot $S(p)$ und Nachfrage $D(p)$ als Funktion des Preises $p$ auf (in unserem Fall ist $S(p)=-\gamma +\delta p$und $D(p)=\alpha - \beta p$).

 

(Das Verfahren funktioniert auch im Falle nichtlinearer Angebots- und Nachfragefuntion.)

Starten in der Peride 0 mit Preis $p_0$ und erhalten wir in der Periode 1 ein Angebot $q_1 = S(p_0)$ (Pfeil nach oben).

Wegen des Marktgleichgewichts (Modellannahme) muß für den Preis $p_1$ gelten, $D(p_1)=q_1$ (Pfeil nach links).

In der nächsten Periode erhalten wir für den Preis $p_1$ ein Angebot $q_2=S(p_1)$ (Pfeil nach unten).

Wegen des Marktgleichgewichts gilt der Preis $p_2$ (Pfeil nach rechts).

Preise und Mengen in aufeinanderfolgenden Perioden durch Wiederholen des Vorganges. Dabei weben wir ein ,,Spinnennetz``, (engl. cobweb) um den Fixpunkt $(\bar{p},\bar{q})$($\bar{q}=S(\bar{p})=D(\bar{p})$).

Je nach Verhältnis von $\beta$ und $\delta$wird die Oszillation immer größer oder kleiner.

Im Grenzfall $\delta = \beta$ erhalten wir eine zyklische Lösung mit $p_0 = p_2 = p_4 = \ldots$.