




previous: Differenzengleichungen erster Ordnung
up: Differenzengleichungen erster Ordnung
next: Homogene lineare Differenzengleichungen
Differenzengleichungen wie in obigem Beispiel
lassen sich durch Iteration berechnen, wenn der
Startwert 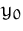 gegeben ist.
gegeben ist.
BEISPIEL
Lösung von 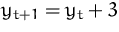 mit
Anfangsbedingung
mit
Anfangsbedingung 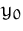 :
:
![\begin{displaymath}
\begin{array}[t]
{l}
y_1 = y_0 + 3\\ y_2 = y_1 + 3 = (y_0+...
... 3 = y_0 + 3\cdot 3\\ \ldots\\ y_t = y_0 + 3\,t
\end{array} \end{displaymath}](img1842.gif)
Die Anfangsbedingung 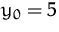 ergibt
ergibt 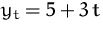 .
.
BEISPIEL
Lösung von 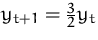 mit
Anfangsbedingung
mit
Anfangsbedingung 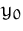 :
:
![\begin{displaymath}
\begin{array}[t]
{l}
y_1 = \frac{3}{2} y_0\\ y_2 = \frac{3...
...\ \ldots\\ y_t = \left(\frac{3}{2}\right)^t y_0
\end{array} \end{displaymath}](img1846.gif)
Die Anfangsbedingung 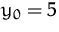 ergibt
ergibt
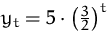 .
.





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![]() gegeben ist.
gegeben ist.
![]() mit
Anfangsbedingung
mit
Anfangsbedingung ![]() :
:
![\begin{displaymath}
\begin{array}[t]
{l}
y_1 = y_0 + 3\\ y_2 = y_1 + 3 = (y_0+...
... 3 = y_0 + 3\cdot 3\\ \ldots\\ y_t = y_0 + 3\,t
\end{array} \end{displaymath}](img1842.gif)
![]() mit
Anfangsbedingung
mit
Anfangsbedingung ![]() :
:
![\begin{displaymath}
\begin{array}[t]
{l}
y_1 = \frac{3}{2} y_0\\ y_2 = \frac{3...
...\ \ldots\\ y_t = \left(\frac{3}{2}\right)^t y_0
\end{array} \end{displaymath}](img1846.gif)