previous: Homogene lineare Differentialgleichung zweiter up: Einfache DG zweiter Ordnung next: Differenzengleichungen

  
Inhomogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten

$\bullet\quad$$\mbox{\ovalbox{$\displaystyle y''(x) + a_1 y'(x) + a_2 y(x) = s$}}$

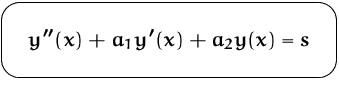
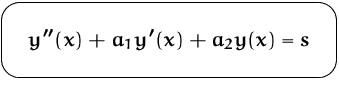
Die Lösung läßt sich stets in der Gestalt

$\mbox{\ovalbox{$\displaystyle y = y_h + y_p$}}$

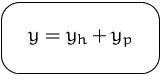
darstellen, wobei

$y_h$ ... allgemeine Lösung der homogenen DG ($s=0$)
$y_p$ ... partikuläre Lösung der inhomogenen DG

Konstante Koeffizienten:

$\mbox{\ovalbox{$\displaystyle y_p(x)=\frac{s}{a_2}$}}$

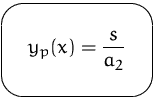
BEISPIEL
Lösung des Anfangswertproblems

$y''(t) + y'(t) - 2y (t) = -10$

$y(0) = 12$, $y'(0) = -2$

homogene DG: $y'' + y' -2y = 0$

$$\lambda^2 + \lambda - 2 = 0 \quad\Rightarrow\quad \lambda_1 = 1, \lambda_2 = - 2$$

Allgemeine Lösung der homogenen DG:

$$y_h (t) = C_1\, e^t + C_2\, e^{-2t}$$

partikuläre Lösung:

$$y_p = \frac{s}{a_2} = \frac{-10}{-2} = 5$$

Allgemeine Lösung:

$$y(t) = C_1\, e^t + C_2\, e^{-2t} + 5$$

Anfangswertproblem:

$$\begin{array} {l} 12= y(0) = C_1 + C_2 + 5\\ -2 = y'(0) = C_1 -2\, C_2 \end{array}$$

$$\Rightarrow C_1=4,\, C_2=3$$

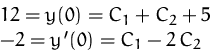
Spezielle Lösung des Anfangswertproblems:

$$y(t) = 4 e^t + 3 e^{-2t} +5$$