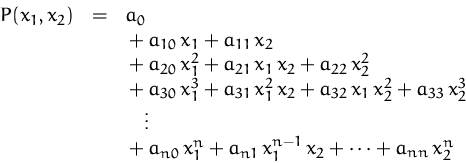
Die Idee der Taylorreihen kann auch für Funktionen in mehreren Variablen verwirklicht werden.
Ein Polynom in zwei Variablen hat die allgemeine Form
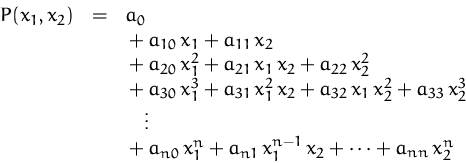
Wenn wir die Funktion ![]() an der Stelle
an der Stelle
![]() nur durch ein Polynom 1. Ordnung approximieren,
dann erhalten wir das totale
Differential und es gilt
nur durch ein Polynom 1. Ordnung approximieren,
dann erhalten wir das totale
Differential und es gilt
![]()
Allgemein gilt für die Koeffizienten
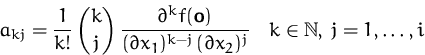
Die Taylorreihe bis zur zweiten Ordnung an der Stelle ![]() lautet
lautet
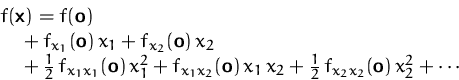
Wir fassen die zweiten partiellen Ableitungen von ![]() an der Stelle
an der Stelle ![]() zu einer
zu einer ![]() -Matrix zusammen.
Diese Matrix wird als Hesse-Matrix von
-Matrix zusammen.
Diese Matrix wird als Hesse-Matrix von ![]() an der Stelle
an der Stelle
![]() bezeichnet.
bezeichnet.
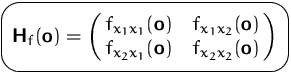
Die quadratischen Glieder der Taylorreihe bilden eine quadratische Form.
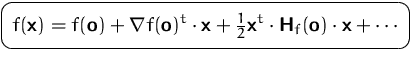
Im allgemeinen Fall mit ![]() Variablen lautet die Hesse-Matrix an der
Stelle
Variablen lautet die Hesse-Matrix an der
Stelle ![]() :
:
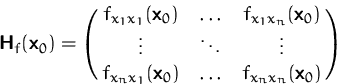
Die Taylorreihe an der Stelle ![]() :
:
![]()
BEISPIEL
Wir suchen das Taylorpolynom 2. Ordnung von
![]()
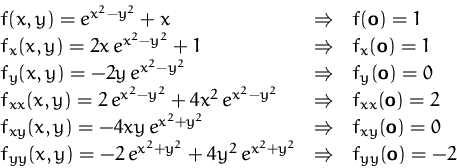
Das Taylorpolynom lautet daher
![\begin{displaymath}
\begin{array}
{ll}
f(\mathsfbf{x})
&\approx f(\mathsfbf{o}...
... }\cdot\pmatrix{x\cr y}\\ [3ex]
&=1+x + x^2-y^2
\end{array} \end{displaymath}](img1285.gif)