previous: Implizite Funktionen up: Funktionen in mehreren Variablen next: Taylorreihen II

Höhere partielle Ableitungen  

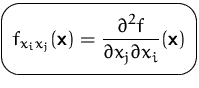
Analog zu den Funktionen in einer Variablen können wir partielle Ableitungen nochmals ableiten und erhalten so  höhere partielle Ableitungen.

Folgende Schreibweisen sind für die zweiten partiellen Ableitungen üblich:

$\mbox{\ovalbox{$\displaystyle f_{x_ix_j}(\mathsfbf{x}) =\frac{\partial^2 f}{\partial x_j\partial x_i}(\mathsfbf{x})$}}$

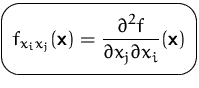
Es kommt dabei auf die Reihenfolge beim Differenzieren (meist!) nicht an. Es gilt (falls alle zweiten partiellen Ableitungen existieren und stetig sind):

$\mbox{\ovalbox{$\displaystyle \frac{\partial^2 f}{\partial x_j\partial x_i}(\mathsfbf{x}) =\frac{\partial^2 f}{\partial x_i\partial x_j}(\mathsfbf{x})$}}$

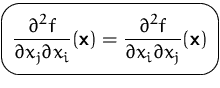
BEISPIEL
Die ersten partiellen Ableitungen von

$$f(x_1,x_2)=x_1^2+3\,x_1\,x_2$$

sind

$$f_{x_1}=2\,x_1+3\,x_2\qquad f_{x_2}=0 + 3\,x_1$$

Die zweiten partiellen Ableitungen sind

$$\begin{array} {ll} f_{x_1 x_1}=2\qquad & f_{x_1 x_2}=3\\ f_{x_2 x_1}=3\qquad & f_{x_2 x_2}=0\\ \end{array}$$