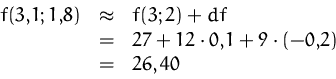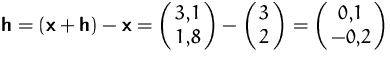Wir wollen eine Funktion ![]() durch eine lineare Funktion
so approximieren, daß der Fehler möglichst klein ist.
Den Funktionswert an einer Stelle
durch eine lineare Funktion
so approximieren, daß der Fehler möglichst klein ist.
Den Funktionswert an einer Stelle
![]() können
wir näherungsweise analog zur Richtungsableitung berechnen.
können
wir näherungsweise analog zur Richtungsableitung berechnen.
![]()
Das totale Differential erhalten wir, wenn wir die ![]() durch
,,unendlich kleine`` Differentiale
ersetzen.
durch
,,unendlich kleine`` Differentiale
ersetzen.
DEFINITION (TOTALES DIFFERENTIAL)
Die lineare Funktion
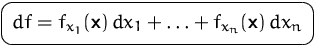
heißt das
totale Differential
von ![]() an der Stelle
an der Stelle ![]() .
.
BEISPIEL
Wir suchen das totale Differential von
![]()
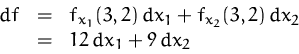
Wir berechnen nun
![]() mit Hilfe des totalen Differentials an der
Stelle
mit Hilfe des totalen Differentials an der
Stelle ![]() .
.