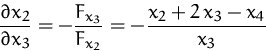Durch ![]() wird eine Abhängigkeit von
wird eine Abhängigkeit von ![]() und
und ![]() definiert ( implizite Funktion).
definiert ( implizite Funktion).
In kleinen Intervallen ist es daher unter Umständen möglich,
![]() als Funktion von
als Funktion von ![]() darzustellen und umgekehrt
( explizite Funktion):
darzustellen und umgekehrt
( explizite Funktion):
![]()
Wenn ![]() eine lineare Funktion ist, dann erhalten wir
(vorausgesetzt
eine lineare Funktion ist, dann erhalten wir
(vorausgesetzt ![]() ):
):
![]()
Wenn ![]() nicht linear ist, dann
können wir die Ableitung von
nicht linear ist, dann
können wir die Ableitung von ![]() berechnen, indem wir die Funktion
lokal durch das totale Differential von
berechnen, indem wir die Funktion
lokal durch das totale Differential von ![]() ersetzen.
ersetzen.
![]()
Daraus erhalten wir
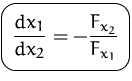
Wir sehen außerdem, daß die Funktion lokal genau dann
existiert, wenn ![]() ist.
ist.
![\begin{figure}
\setlength {\unitlength}{1.3mm}
\begin{picture}
(50,50)
\thin...
..._1,x_2) = x^2 + y^2 - 1 = 0\end{displaymath}\mbox{}\\ [-10ex]\mbox{}\end{figure}](img1257.gif)
Das gleiche könne wir nun mit Funktionen in mehreren Variablen machen.
Durch ![]() erhalten wir wieder eine implizite
Funktion. Es ist nun (meist) wieder möglich, die Variable
erhalten wir wieder eine implizite
Funktion. Es ist nun (meist) wieder möglich, die Variable
![]() als Funktion aller anderen Variablen darzustellen:
als Funktion aller anderen Variablen darzustellen:
![]()
Durch das totale Differential können wir etwa die partiellen Ableitung
von ![]() nach
nach ![]() berechnen:
berechnen:
![]()
Wir erhalten
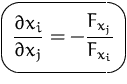
BEISPIEL
Gesucht ist ![]() der impliziten
Funktion
der impliziten
Funktion
![]()
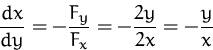
BEISPIEL
Gesucht ist ![]() der impliziten Funktion
der impliziten Funktion
![]()