previous: Das totale Differential up: Funktionen in mehreren Variablen next: Die Kreuzpreiselastizität

Partielle Elastizitäten  

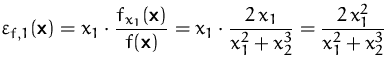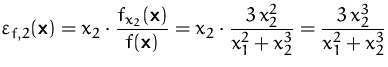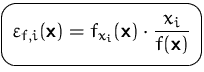
Die  partiellen Elastizitäten geben relative Änderungsraten bezüglich den einzelnen Variablen an.

$\mbox{\ovalbox{$\displaystyle \varepsilon_{f,i}(\mathsfbf{x}) =f_{x_i}(\mathsfbf{x})\cdot\frac{x_i}{f(\mathsfbf{x})}$}}$

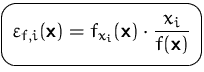
Die partielle Elastizität $\varepsilon_{f,i}(\mathsfbf{x})$ gibt ungefähr an, um wieviel Prozent sich der Funktionswert $f(\mathsfbf{x})$ ändert, wenn sich die $i$-te Variable um $1\%$ ändert und die anderen Variablen unverändert bleiben.

BEISPIEL
Gesucht sind die partiellen Elastizitäten von

$$f(x_1,x_2)=x_1^2+x_2^3$$

$$\varepsilon_{f,1}(\mathsfbf{x})=x_1\cdot\frac{f_{x_1}(\mathsfbf{... ...mathsfbf{x})} =x_1\cdot\frac{2\,x_1}{x_1^2+x_2^3}=\frac{2\,x_1^2}{x_1^2+x_2^3}$$

$$\varepsilon_{f,2}(\mathsfbf{x})=x_2\cdot\frac{f_{x_2}(\mathsfbf{... ...thsfbf{x})} =x_2\cdot\frac{3\,x_2^2}{x_1^2+x_2^3}=\frac{3\,x_2^3}{x_1^2+x_2^3}$$