Die erste Ableitung einer Funktion gibt die Änderungsrate
einer Funktion ![]() an der Stelle
an der Stelle ![]() in absoluten Zahlen an.
Sie ist somit abhängig von der Skalierung
von Argument und Funktionswert.
in absoluten Zahlen an.
Sie ist somit abhängig von der Skalierung
von Argument und Funktionswert.
Diese relative Änderung der Funktion erhalten wir durch

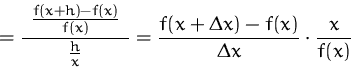
bzw. für die marginale Änderungsrate
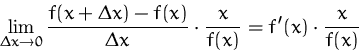
DEFINITION (ELASTIZITäT)
Der Ausdruck
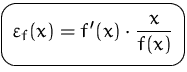
heißt die Elastizität von ![]() an der Stelle
an der Stelle ![]() .
.
BEISPIEL
Sei ![]() . Dann ist
. Dann ist
![]()
DEFINITION ()
Eine Funktion ![]() heißt in
heißt in ![]()
elastisch,
falls
![]()
1-elastisch,
falls
![]()
unelastisch,
falls
![]()
Für eine elastische Funktion gilt daher: ändert sich das Argument um
![]() , so ändert sich der Funktionswert um mindestens
, so ändert sich der Funktionswert um mindestens ![]() .(Die Aussage gilt streng genommen nur für das totale Differential von
.(Die Aussage gilt streng genommen nur für das totale Differential von
![]() .)
.)
BEISPIEL
In welchen Punkten ist ![]() 1-elastisch?
1-elastisch?
![]()
In welchen Punkten ist ![]() elastisch?
elastisch?
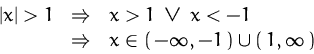
In welchen Punkten ist ![]() unelastisch?
unelastisch?
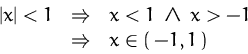
BEISPIEL
Sei ![]() eine elastische Nachfragefunktion,
eine elastische Nachfragefunktion, ![]() der
Preis. Wir können voraussetzen, daß
der
Preis. Wir können voraussetzen, daß ![]() und
und ![]() und
daß
und
daß ![]() monoton fallend ist.
Also gilt
monoton fallend ist.
Also gilt
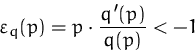
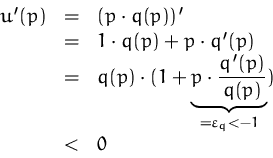
Analog erhalten wir, daß
![]() , wenn
, wenn ![]() unelastisch ist, und
unelastisch ist, und
![]() , wenn
, wenn ![]() 1-elastisch ist.
1-elastisch ist.