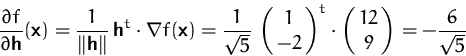previous: Der Gradient up: Funktionen in mehreren Variablen next: Das totale Differential

Die Richtungsableitung  

Die partielle Ableitung der Funktion
$f(\mathsfbf{x})=f(x_1,\ldots,x_i,\ldots,x_n)$ nach der $i$-ten Variable $x_i$ haben wir folgendermaßen erhalten:

Sei $\mathsfbf{h}=\mathsfbf{e}_i$ (der $i$-te Einheitsvektor). Wir definieren eine Funktion

$$\tilde f_\mathsfbf{h}(t)=f(x_1,\ldots,x_i+t,\ldots,x_n) =f(\mathsfbf{x}+t\cdot\mathsfbf{h})$$

und differenzieren diese:

$$\frac{\partial f}{\partial x_i} (\mathsfbf{x}) =\left. \frac{d \tilde f_i}{dt} \right\vert_0 = \tilde f'_\mathsfbf{h}(0)$$

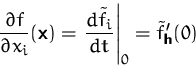
Wir können die partiellen Ableitungen verallgemeinern, indem wir für $\mathsfbf{h}$ einen beliebigen Vektor mit Länge 1 zulassen.

Diese Ableitung gibt dann die Änderung von $f$ an, wenn wir $\mathsfbf{x}$ in Richtung $\mathsfbf{h}$ verschieben.

Sie heißt die  Richtungsableitung $\frac{\partial f(\mathsfbf{x})}{\partial\mathsfbf{h}}$ von $f$ in Richtung $\mathsfbf{h}$.

Es gilt (für $\Vert\mathsfbf{h}\Vert=1$):

$$\frac{\partial f}{\partial\mathsfbf{h}}(\mathsfbf{x}) =f_{x_... ...athsfbf{x})\cdot h_n =\nabla f(\mathsfbf{x})^t\cdot\mathsfbf{h}$$

Falls $\mathsfbf{h}$ nicht Norm 1 hat, muß zuerst normiert werden:

$\mbox{\ovalbox{$\displaystyle \frac{\partial f}{\partial\mathsfbf{h}}(\mathsfbf... ...=\frac{1}{\Vert\mathsfbf{h}\Vert}\,\mathsfbf{h}^t\cdot\nabla f(\mathsfbf{x})$}}$

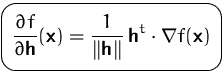
BEISPIEL
Wir suchen die Richtungsableitung von

$$f(x_1,x_2)=x_1^2+3\,x_1\,x_2$$

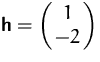nach $\mathsfbf{h}=\pmatrix{1\cr -2}$ an der Stelle $\mathsfbf{x}=\pmatrix{3\cr 2}$.

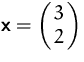Norm von $\mathsfbf{h}$: $\Vert\mathsfbf{h}\Vert = \sqrt{\mathsfbf{h}^t\,\mathsfbf{h}} = \sqrt{1^2+(-2)^2} = \sqrt{5}$.

Die Richtungsableitung lautet daher

$$\frac{\partial f}{\partial\mathsfbf{h}}(\mathsfbf{x}) = \fr... ...trix{1\cr -2}^t\cdot \pmatrix{12\cr 9} = -\frac{6}{\sqrt{5}}$$