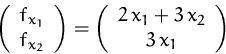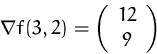previous: Partielle Ableitungen up: Funktionen in mehreren Variablen next: Die Richtungsableitung

Der Gradient  

Wir fassen die partiellen Ableitungen erster Ordnung zu einem Vektor, dem Gradienten an der Stelle $\mathsfbf{x}$, zusammen.

DEFINITION (GRADIENT)
Der Vektor

$\mbox{\ovalbox{$\displaystyle \nabla f(\mathsfbf{x})= \left(\begin{array} {c} f_{x_1}(\mathsfbf{x})\\ \vdots\\ f_{x_n}(\mathsfbf{x})\\ \end{array}\right)$}}$

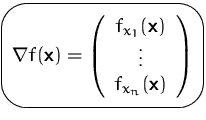
heißt der  Gradient von $f$ an der Stelle $\mathsfbf{x}$.

Der Gradient einer Funktion $f$ im Punkt $\mathsfbf{x}$ zeigt in die Richtung des steilsten Anstieges von $f$.Seine Länge gibt diese Steigung an.

Der Gradient ist die Verallgemeinerung der ersten
(gewöhnlichen) Ableitung von Funktionen in einer Variablen auf Funktionen in mehreren Variablen.

BEISPIEL
Der Gradient von

$$f(x_1,x_2)=x_1^2+3\,x_1\,x_2$$

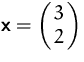an der Stelle $\mathsfbf{x}=\pmatrix{3\cr 2}$ ist:

$$\left( \begin{array} {c} f_{x_1}\\ f_{x_2} \end{array} \r... ...begin{array} {c} 2\,x_1+3\,x_2\\ 3\,x_1 \end{array} \right)$$

$$\nabla f(3,2)= \left( \begin{array} {c} 12\\ 9 \end{array} \right)$$