previous: Die zusammengesetzte Funktion up: Spezielle Funktionen next: Elementare Funktionen

Die Umkehrfunktion oder inverse Funktion  

Die Zuordnungsvorschrift der inversen Abbildung einer reellen Funktion erhalten wir durch Vertauschen der Rollen von Argument ($x$) und Bild ($y$). Mit anderen Worten, wir drücken $x$ als Funktion von $y$ aus.

BEISPIEL
Wir suchen die Umkehrfunktion von

$y=f(x)=2x-1$

Durch Umformung erhalten wir:

$y=2x-1\,\Leftrightarrow\,y+1=2x\,\Leftrightarrow\, \frac{1}{2}(y+1)=x$

Die Umkehrfunktion lautet daher $f^{-1}(y)=\frac{1}{2}(y+1)$. Da es üblich ist, das Argument mit $x$ zu bezeichnen, schreiben wir

$f^{-1}(x)=\frac{1}{2}(x+1)$

BEISPIEL
Die Umkehrfunktion von $f(x)=x^3$ ist $f^{-1}(x)=\sqrt[3]{x}$.

Das Vertauschen von $x$ und $y$ spiegelt sich auch im Graphen der Umkehrfunktion wieder.

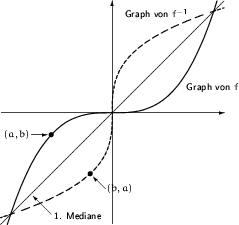
(Graph der Funktion $f(x)=x^3$ und ihrer Inversen.)

Die Inverse einer Funktion muß nicht immer existieren.

BEISPIEL
Die Funktion

$f\colon{\mathbb R}\to{\mathbb R},\,x\mapsto f(x)=x^2$

besitzt keine Inverse.

Definitions- und Wertemenge sind Teil einer Funktion.

So ist z.B. die Funktion

$f\colon{\mathbb R}^+\to{\mathbb R}^+,\,x\mapsto x^2$

bijektiv und besitzt sehr wohl eine Umkehrfunktion, nämlich

$f^{-1}\colon{\mathbb R}^+\to{\mathbb R}^+,\,x\mapsto\sqrt{x}$.