




previous: Die Einheitsfunktion oder identische
up: Spezielle Funktionen
next: Die Umkehrfunktion oder inverse
Seien 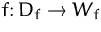 und
und 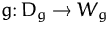 Funktionen mit
Funktionen mit
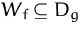 .Dann heißt die Funktion
.Dann heißt die Funktion
zusammengesetzte Funktion (,,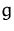 zusammengesetzt
zusammengesetzt 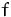 ``).
``).
BEISPIEL
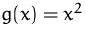 ,
, 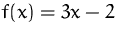 . Dann ist
. Dann ist
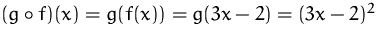





© 1997,
Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
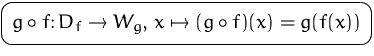
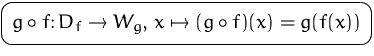
![]() zusammengesetzt
zusammengesetzt ![]() ``).
``).
![]() ,
, ![]() . Dann ist
. Dann ist ![]()